
こんにちは。タクマ™ [@suwaru_blog] です。
ぶっちゃけ、木とグラフの問題は面倒くさいです。
だからこそエンジニア面談、競技プログラミングでは多く出題されています。
今回は「木とグラフについて、実装方法と探索アルゴリズム」を徹底解説します!
木の種類

木とは、連結グラフの一種であり、ノードで構成されるデータ構造です。
木の学習では、以下のことを意識しましょう。
- 木の探索の計算時間では、最悪ケース・平均ケースで結果が大きく異なります
- 最悪ケース・平均ケース、両方の観点で評価できるようになりましょう
- 木とグラフはゼロから実装できるようになりましょう
つづいて、木の特徴を挙げます。
- 通常、木は root (根) ノードを持ちます
- root ノードは 0 個以上の子ノードを持ちます
- 各子ノードは 0 個以上の子ノードを持ちます
- それら子ノード以下も同様に子ノードを持ちます
- 木は閉路がありません (出発点に戻ることはない)
- ノードの順序
- 特別な順序の場合、そうでない場合があります
- ノードの値
- どんな型でも持つことができます
- 親ノードへ遡るリンク
- 持っている場合、そうでない場合があります
// シンプルな Node クラス定義
class Node {
public String name;
public Node[] children;
}
// Node をラップする Tree クラスを定義してもよい
class Tree {
public Node root;
}
二分木 (Binary Tree) とは
二分木とは、各ノードが最大 2 個の個しか持たない木です。
すべての木が二分木というわけではありません。
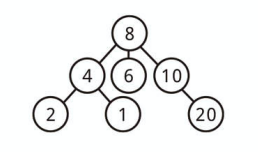
たとえば、以下の木は「三分木」といえます。
二分木ではない木を使う場合は多々あります。
たとえば、たくさんの電話番号を木で表現してみましょう。
各ノードは (それぞれ 1 桁分を意味する) 最大 10 個の子ノードの 10 分木を使うことになります。
葉ノードとは
子ノードを持たないノードは「葉ノード」と呼ばれます。
二分探索木 (BST) とは
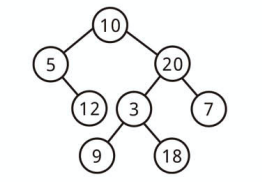
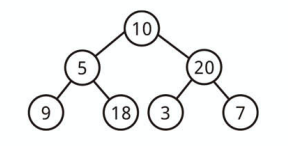
二分探索木とは、すべてのノードが特定の並び順になっている二分木のことです。
特定の並び順とは すべての左の子孫 <= n <= すべての右の子孫 を意味します。
この不等式は「各ノード直下の子だけではなく、すべての子孫で成り立っていないといけない」という点に注意してください。
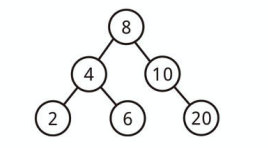
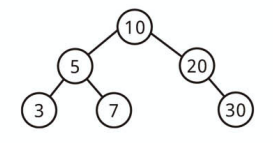
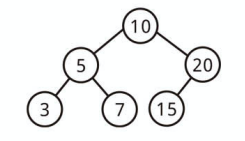
上記は二分探索木です。
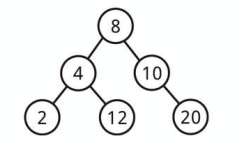
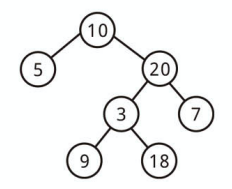
上記は 12 が 8 よりも左にあるので、二分探索木ではありません。
二分探索木では「左側の子孫すべてが現在のノード以下であり、右側の子孫すべてが現在のノード以上である」制約を持たせているのです。
なお、二分探索木の定義によっては重複する値を持たないことがあります。
重複する値がある場合、右側・左側どちらにもある場合があります。
平衡と非平衡
多くの木は平衡になっています。
平衡木とは、極端にアンバランスではない木と思っていれば大丈夫です。
データの追加や検索が O(log n) で実行できれば OK です。
左右の部分木がちょうと同じサイズ…という意味ではないので注意しましょう。
一般的な平衡木
ここでは詳しくは説明しませんが、平衡木の一般的な形は 2 種類あります。
- 赤黒木
- AVL 木
全二分木 (Full Binary Tree) とは
すべてのノードが 0 個か 2 個の子を持つ二分木のことです。
つまり、子を 1 個だけしか持たないノードは存在しません。
上記は全二分木ではありません。
上記は全二分木です。
完全二分木とは
日本語に訳すると同じ「完全二分木」ですが、完全二分木の種類は 2 つあります。
- Complete Binary Tree
- Perfect Binary Tree
Complete Binary Tree とは
一番深いノード以外のすべてのノードが満たされている二分木のことです。
最深部の一番右側のノードまで完全に埋まっている状態を意味します。
上記は Complete Binary Tree ではありません。
上記は Complete Binary Tree です。
Perfect Binary Tree とは
全二分木と Complete Binary Tree の性質を満たす二分木のことです。
すべての葉ノードは同じ深さであり、最も深い部分のノード数は最大になっています。
k を深さとすると、ノード数はちょうど 2^k - 1 個になります。
上記は Perfect Binary Tree です。
なお Perfect Binary Tree はレアケースということを覚えておいてください。
二分木の走査

二分木の走査 (traversal) の実装をみていきましょう。
間順走査 (In-Order Traversal) とは
最も一般的な二分木の走査です。
左側の枝、現在ノード、右側の枝で訪れることを意味します。
In-Order とは「中央順」という意味ですが、訪問するノードが昇順になるのが特徴です。
void inOrderTraversal (TreeNode node) {
if (node != null) {
// 再起実行 (左側の枝)
inOrderTraversal(node.left);
// 現在のノード
visit(node);
// 再起実行 (右側の枝)
inOrderTraversal(node.right);
}
}
前順走査 (Pre-Order Traversal) とは
Pre-Order とは「先行順」という意味ですが、現在ノードを訪れてから子ノードを訪れます。
必ず root (根) ノードから訪れるのが特徴です。
void preOrderTraversal (TreeNode node) {
if (node != null) {
// 現在のノード
visit(node);
// 再起実行 (左側の枝)
preOrderTraversal(node.left);
// 再起実行 (右側の枝)
preOrderTraversal(node.right);
}
}
後順走査 (Post-Order Traversal) とは
Post-Order とは「後行順」という意味ですが、子ノードを訪れてから現在ノードを訪れます。
void postOrderTraversal (TreeNode node) {
if (node != null) {
// 再起実行 (左側の枝)
postOrderTraversal(node.left);
// 再起実行 (右側の枝)
postOrderTraversal(node.right);
// 現在のノード
visit(node);
}
}
二分ヒープとは
最小ヒープとは
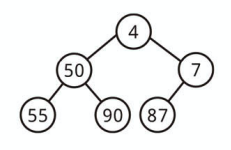
すべてのノードが子ノードよりも小さい完全二分木 (Complete Binary Tree) が最小ヒープです。
つまり root (根) ノードが木全体の最小値を持ちます。
左右の順序は決まっていません。
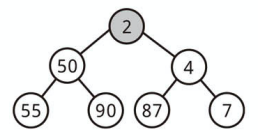
ノードを挿入する
完全二分木の特性上、ノードの挿入は「常に最後の部分に要素を追加する」ところから始まります。
次に、適切な位置が見つかるまで、新たに加えたノードと親ノードを入れ替えて木を修正します。
最小の要素が一番上にくるようにしましょう。
ヒープ内のノード数を n とすると、実行時間は O(log n) になります。
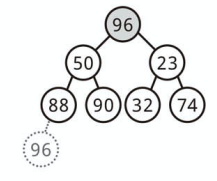
最小要素を取り出す
最小ヒープから最小要素を見つけるのは簡単です。
常に最小要素は一番上にあるからです。
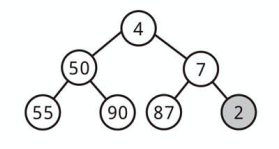
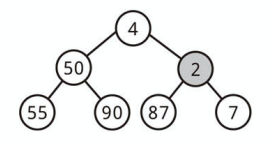
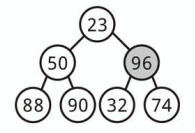
ただし取り除くためには、最小要素とヒープ末尾の要素 (一番右下) を入れ替えます。
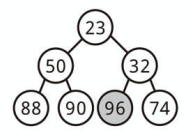
次にその要素と子要素を入れ替えながら、適切な位置まで下ろしていきます。
最小ヒープでは左右の順序が決まっていませんが、
上に最小値を持っていきたいので小さい方の値と交換しながら下ろします。
ヒープ内のノード数を n とすると、実行時間は O(log n) になります。
最大ヒープとは
最大ヒープは本質的には同じものですが、要素の並び順が降順になっています。
トライ木 (プレフィックス木) とは

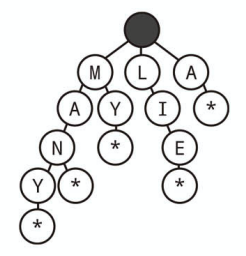
トライ木 (プレフィックス木) とは、各ノードに文字が保持される n 分木の一種です。
木を下っていくと、その経路が単語になります。
* ノードとは
完全な単語であることを示すために * 文字を持った「 * ノード」を使うことがあります。
※ または null を持った「 null ノード」を使うこともあります。
たとえば MANY の下に * ノードがあれば MANY が完全な単語であることを示します。
* ノードの実装
ノードは TrieNode クラスから派生した TerminatingTrieNode クラスを用意するとか、
親ノード内で終端を表すフラグを使えば実装できます。
子ノードの数はどの場所でも「 0 からアルファベットサイズ + 1 」になります。
用途
接頭辞検索用の英語を保持する
よくある使い方としては、接頭辞検索用の英語を保持することです。
ハッシュテーブルでは、文字列が「正しい単語かどうか」素早く検索できますが、
文字列が「正しい接頭辞を持つかどうか」の判別はできません。
そのような場合にトライ木を使うと、文字列の長さが K とすると O(K) で実行できます。
※ すべての文字を読み込む必要があるため、ハッシュテーブルの場合でも O(K) になります。
正しい単語のリスト含む問題
正しい単語のリスト含む問題の多くはトライ木を利用します。
- まず
Mを検索する - 次に
MAを検索する - 次に
MANを検索する - 次に
MANYを検索する
…といった、文字列の接頭辞を繰り返し検索する状況では、
現在のノードにそれまでの経路の参照を渡していきます。
そうすると、その都度 root (根) ノードから検索しなくても、Y が MAN の子であるか調べるだけでよくなります。
グラフの種類

グラフとは、ノード同士のいくつかに「辺」を持ったものの集まりです。
- 有向・無向
- グラフは有向の辺 (一方通行) のものがあります
- 「トポロジカルソート」というソートアルゴリズムが有名
- 「ダイクストラ法」という 2 地点間の最短経路を求める方法がある
- グラフは無向の辺 (双方通行) のものもあります
- グラフは有向の辺 (一方通行) のものがあります
- 複数の孤立した部分グラフから成り立つグラフもあります
- 連結グラフ
- 2 頂点同士にも経路が存在する場合は「連結グラフ」と呼ばれます
- 閉路がある場合、閉路がない場合があります
- 閉路がないグラフは「非巡回グラフ」と呼ばれます
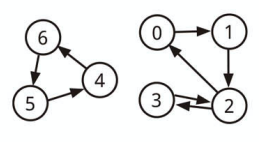
視覚的にグラフを表現すると上記のようになります。
隣接リストとは
グラフをプログラミングで表現する一般的な方法は「隣接リスト」です。
すべての頂点 (ノード) は隣接する頂点のリストを持ちます。
無向グラフでは (a, b) のように辺が 2 回保持されます。
1 回は a の隣接点で、もう 1 回は b の隣接点です。
class Graph {
public Node[] nodes;
}
class Node {
public String name;
public Node[] children;
}
木の場合と異なり、Graph クラスは単一ノードからすべてのノードに到達するとは限りません。
配列・配列リスト・連結リストであったり、ハッシュテーブルで隣接リストを持つことができます。
上記グラフは次のように表現することができます。
| ノード | 参照先ノード |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 0, 3 |
| 3 | 2 |
| 4 | 6 |
| 5 | 4 |
| 6 | 5 |
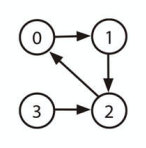
隣接行列とは
隣接行列とは、ノード数を N とすると N*N のブーリアン型行列のことです。matrix[i][j] が真のとき、ノード i からノード j への辺が存在することになります。
無向グラフの場合、行列は対照的になりますが、
有向グラフの場合、行列が対照的になるとは限りません。
| ノード | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 |
グラフ探索

これから紹介するグラフアルゴリズムは隣接リストで使うことができますが、
隣接行列の場合だと少し効率が落ちてしまいます。
隣接リストの場合、隣接するノードの走査を行うことができますが、
隣接行列の場合、全ノードを走査してノードが隣接しているかどうか調べる必要があるからです。
深さ優先探索 (Depth-First Search: DFS) とは
深さ優先探索 (DFS) では、root (根) ノードから探索を開始します。
そして次の枝に移る前に、各枝を完全に探索します。
つまり横方向より、縦方向の (より深い方向の) 探索を優先します。
DFS の優先順位
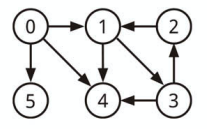
上記グラフの Node[0] から深さ優先探索をしたら、
走査する順番は以下のようになります。
- Node[0]
- Node[1]
- Node[3]
- Node[2]
- Node[4]
- Node[3]
- Node[1]
- Node[5]
DFS の実装
DFS では、ノード a に隣接するノード b に訪れるとき、
a に隣接している他の隣接ノード c などより、先に b に 隣接するノード全てを探索します。
一般的な木の走査や pre-oreder は DFS の一種ですが、
DFS における、木とグラフの違いは「そのノードをすでに訪れたかチェックするかどうか」です。
チェックしていないと無限ループにはまる可能性があります。
void dfs(Node root) {
if (root == null) {
return;
}
visit(root);
root.visited = true;
// 隣接ノードを取り出す
foreach (Node n in root.adjacent) {
if (n.visited == false) {
// 再起実行
dfs(n);
}
}
}
DFS のメリット
深さ優先探索は「グラフのすべてのノードを走査したい」場合に好まれます。
幅優先探索 (Breadth-First Search: BFS) とは
幅優先探索 (BFS) では、root (根) ノードから探索を開始します。
そして子ノードの探索をする前に、現在の隣接ノードを探索します。
つまり縦方向より、横方向の (幅広い方向の) 探索を優先します。
BFS の優先順位
上記グラフの Node[0] から幅優先探索をしたら、
走査する順番は以下のようになります。
- Node[0]
- Node[1]
- Node[4]
- Node[5]
- Node[3]
- Node[2]
BFS の実装
BFS が再帰的な処理であると考えるのは間違いです。
BFS では「キュー」を利用します。
BFS では、ノード a を訪れるとき、
ノード a に隣接するノード b, c などの隣接ノードより、先に a の隣接ノード b, c を訪れます。
void bfs(Node root) {
Queue queue = new Queue();
root.marked = true;
// キューの末尾に加える
queue.enqueue(root);
while (!queue.isEmpty()) {
// キューの先頭から取り除く
Node r = queue.dequeue();
// 隣接ノードを取り出す
foreach (Node n in r.adjacent) {
if (n.marked == false) {
n.marked = true;
queue.enqueue(n);
}
}
}
}
BFS のメリット
幅優先探索は「 2 つのノード間の最短経路、あるいは任意の経路を求めたい」場合に好まれます。
DFS と BFS の比較

たとえば、世界全体のすべての友人関係をグラフで表すことにしましょう。
そしてアッシュとベネッサの友人関係を表す経路を見つけたい場合、
DFS と BFS どちらのアルゴリズムがよいでしょうか。
DFS の場合
深さ優先探索を使った場合は アッシュ → ブライアン → カールトン → デイヴィス → エリック → ファラ → ゲイル → ハリー → イザベラ → ジョン → カリ → ... と非常に長くなってしまいます。
アッシュとベネッサが友人であることを認識しないで検索しているようなものです。
いつか経路は見つかりますが、非常に時間がかかりますし、最短経路ではありません。
BFS の場合
幅優先探索を使った場合、最初のアッシュから出来るだけ近いところに留まって検索します。
まずアッシュの知人をたくさん調べて、どうしても必要なときだけ遠い人間関係も調べます。
アッシュとベネッサが親友、または友人の友人くらいの関係ならすぐに見つけられるでしょう。
- DFS
- 最初のノードに隣接するノードが後回しになる
- かなり遠くまで探索する可能性がある
- BFS
- 最短経路を見つけることができる
双方向探索 (Bidirectional Search) とは
双方向探索では、元となるノードと目的となるノードの最短経路を見つけます。
基本的には「幅優先探索」を元のノードと目的のノード 2 ヶ所から同時に行います。
探索時にお互いが衝突すれば経路発見となります。
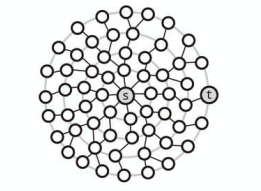
上記は幅優先探索です。
単一の探索では s から t まで深さ 4 だとわかります。
上記は双方向探索です。
s からの探索と t からの探索、つまり双方向の探索があります。
s から t の深さ 2、t から s の深さ 2 のところで互いの探索が衝突します。
そのとき深さの和は 4 だとわかります。
双方向探索が早い理由
各ノードが隣接ノード k 個を持ったグラフがあるとします。
そのときノード s からノード t までの最短経路が d としましょう。
- 通常の幅優先探索の場合
- 最初の深さでは
k個のノードを調べる必要がある - 次の深さでは
k^2個のノードを調べる必要がある (たった深さ 2 なのに…)- 最初の k ノードそれぞれの k 個のノードを探索するため
- これを d 回行うと O(k^d) 個のノードを調べる必要がある
- 最初の深さでは
- 双方向探索の場合
- 2 つの探索は経路の中間地点で衝突します
- つまり、だいたい
d/2の深さで衝突します
- つまり、だいたい
- s からの探索は
k^d/2個のノードを調べる必要がある - t からの探索も
k^d/2個のノードを調べる必要がある - 合計のノード数は
2k^d/2個です- BigO 記法だと O(k^d/2) になります
- 幅優先探索では
k^dかかっていたが、これは(k^d/2) * (k^d/2)の結果と同じである- つまり、双方向探索は幅優先探索の
k^d/2倍早い
- つまり、双方向探索は幅優先探索の
- 2 つの探索は経路の中間地点で衝突します
双方向探索が早い理由
- 幅優先探索
- 「友達の友達」の経路を探索するシステム
- 双方向探索
- 「友達の友達の友達の友達」の経路を探索するシステム
- だいたい 2 倍の長さの経路を検索できるイメージです
CS シリーズ
次回
(ちょっとまってね)
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事



 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント