
こんにちは。iQeda [@iQeeeda] です。
前回、パリティについて解説しました。
今回はその応用編で、偶奇を使った「グラフ理論」について解説します。
目次
ケーニヒスベルグの橋
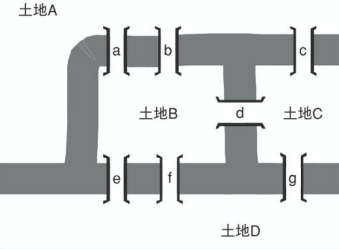
哲学者カントの故郷ケーニヒスベルグには、
川で区切られた 4 つの土地・土地を結ぶ 7 つの橋がありました。
以下の条件で 7 つの橋すべてを渡りつくすことはできるでしょうか?
- 一度でも渡った橋は二度と通れない
- それぞれの土地は何度でも降り立ってよい
- どの土地からスタートしてもよい
- ゴールはどの土地でもよい
また、渡りつくすことはできない場合、それをどうやって証明すればよいでしょうか?
グラフ理論
数学者オイラーはこの問題を解き明かし、それはグラフ理論と呼ばれています。
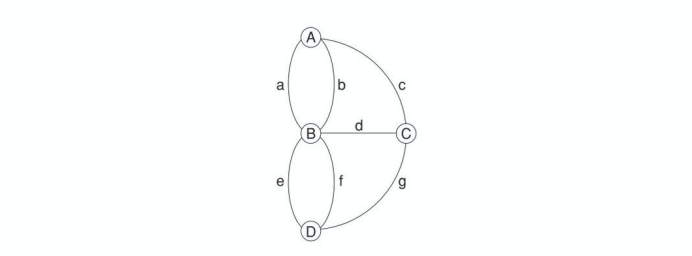
グラフ理論に従い、土地の繋がり方を図式化 (グラフ化) してみましょう。
土地 A, B, C, D のことを「頂点」と呼び、
頂点どうしを結ぶ橋 a, b, c, d, e, f, g のことは「辺」と呼ぶことにします。
次数
頂点からは複数の辺が伸びています。
頂点から伸びている辺の数を「次数」と呼ぶことにします。
また次数が偶数の頂点は「偶点」、次数が奇数の頂点は「奇点」と呼ぶことにします。
減らし歩き
頂点は次数を消費します。
- 頂点からスタートするときは、出口の辺だけ必要
- 次数が 1 必要
- 頂点を経由するには、入口の辺・出口の辺が必要
- 次数が 2 必要
- 頂点にゴールするときは、入り口の辺だけ必要
- 次数が 1 必要
通った辺にチェックをつけて、その頂点の次数を減らすという考え方です。
次数が減るということは「偶点・奇点が変化する可能性がある」ので、それもチェックします。
このテクニックを「減らし歩き」と呼ぶことにします。
| 頂点 | 次数 | 偶奇 |
|---|---|---|
| スタート時の頂点 | 次数を 1 減らす | 変化しない |
| 経由する頂点 | 次数を 2 減らす | 偶点は奇点・奇点は偶点に変化 |
| ゴール時の頂点 | 次数を 1 減らす | 変化しない |
一筆書きできるということは「すべての頂点の次数が 0 になる」ということ
一筆書きできるということは、減らし歩きの結果「すべての頂点の次数が 0 になる」を意味します。
奇点があったら、その頂点には通っていない辺が残っています。
経由する頂点を 0 (偶点) にするには、
それぞれの頂点が「元々偶点である」必要があります。
なぜなら経由するとき、偶奇は変化しないからです。
スタート・ゴールの頂点が一致する場合
スタート・ゴールの頂点が一致する場合…
スタート・ゴール時の頂点を 0 (偶点) にするには、
その頂点は「元々偶点である」必要があります。
なぜならスタートするとき・ゴールするときで、その頂点の次数が 1 ずつ減るので、
次数が合計 2 減ることになり、最終的な偶奇は変化しないためです。
つまり、スタート・ゴールの頂点が一致する場合は「すべての頂点が遇点である」必要があります。
スタート・ゴールの頂点が一致しない場合
スタート・ゴールの頂点が一致しない場合…
スタート・ゴール時の頂点を 0 (偶点) にするには、
それぞれの頂点が「元々奇点である」必要があります。
なぜならスタートするとき・ゴールするときで、それぞれの頂点の次数が 1 ずつ減るので、
最終的な偶奇が変化するためです。
つまり、スタート・ゴールの頂点が一致しない場合は「奇点が 2 個である」必要があります。
答え
一筆書きの条件は「すべての頂点が偶点」または「奇点が 2 個」であることがわかりました。
含意の論理をつかうと 一筆書きができる ⇒ (ならば) 「すべての頂点が偶点」または「奇点が 2 個」 です。
- 頂点 A の次数は 3
- 奇点
- 頂点 B の次数は 5
- 奇点
- 頂点 C の次数は 3
- 奇点
- 頂点 D の次数は 3
- 奇点
奇点が 4 つであることを理由に「橋を渡りつくすことはできない」を証明することができます。
重要なことは、全パターン試行錯誤しなくても「不可能であることを証明できる」です。
オイラーは辺の数そのものではなく、辺の「偶奇」に注目しました。
これも前回の記事で紹介したパリティのチェックの一種です。
CS シリーズ
次回
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント