
こんにちは。iQeda [@iQeeeda] です。
今回は「配列・文字列」問題の解説をします。
また、前提知識である「ハッシュテーブル・配列リスト・文字列連結」の説明をしています。
問題を解くことで「ビットベクトル・行列」の知識も身につけることができると思います。
目次
「配列・文字列」を扱う問題の傾向
「配列」の扱いについて述べている問題が、別の問題では「文字列」の問題として問われることがあります。逆もまた然りです。
配列・文字列の問題は「置き換えられて出題されることがある」点をまず知っておきましょう。
ハッシューテーブルとは

ハッシューテーブルとは、
効率的な検索を行うために「キーをハッシュ値にマッピングするデータ構造」です。
プログラミング言語によっては「辞書型」と呼ばれるものです。
それはどのように実装されているのか?考えてみましょう。
ハッシュテーブルの一般的な実装方法
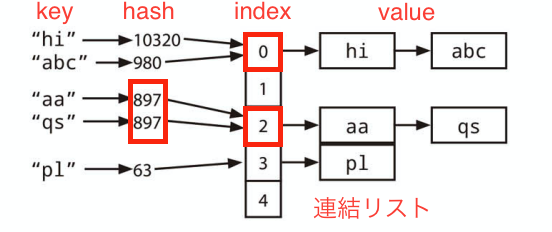
「連結リストを要素にもった配列」と「ハッシュ関数」を使うのが一般的で単純な実装です。
キーと値を挿入するために次のことを行います。
- キーからハッシュ値を計算する
- ハッシュ値から Array の index を計算する
- Array の value にはデータ構造が「連結リスト」のオブジェクトを格納する
- 連結リストは (必要があれば) 複数の value を持たせることが可能
- これで key に対応する value を探すことができるようになる
もう少し詳しく説明します。
- 通常、キーのハッシュ値は int 型か long 型の整数を使う
- 無限の「キー」と有限の「整数値」が存在することになる
- このとき、2 つのキーが同じハッシュ値を持ってしまう場合がある
- hash 値の衝突
- ハッシュ値を配列の index に対応させる
hasy(key) % (配列の長さ)のような計算で index を作成する- このとき、異なる 2 つのハッシュ値が同じ index に対応してしまう場合がある
- index 値の衝突
- 配列の index の指す場所に連結リスト (キーと値) を作成する
- こういった値の衝突に備えるため、連結リストを使うことになっている
- 異なる 2 つのキーが同じハッシュ値の場合
- 異なる 2 つのハッシュ値が同じ index に対応してしまったの場合
- こういった値の衝突に備えるため、連結リストを使うことになっている
ハッシュテーブルの実行時間
値の衝突が大きい場合、実行時間はキーの数を N とすると O(N) になります。(最悪ケース)
しかし、実装を最適化すると衝突は最小限に抑えられるので O(1) にすることが可能です。
またハッシュテーブルを「二分探索木」で実装すると O(log N) になります。
順番に走査可能で、大きな配列を使わない場合は省スペースになるというメリットがあります。
【Java】HashSet オブジェクト
もちろん自分で実装しなくても、
通常のプログラミング言語はハッシュテーブルオブジェクトを用意しています。
たとえば Java の場合は HashSet というオブジェクトがあり、以下のような特徴があります。
- 要素として null を格納できる
- 要素の重複不可
- 同じ値の要素を複数もつことができない
- 要素の順番は保証されない
- 追加した順番は関係ない
配列リスト (可変長配列) とは

プログラミング言語によっては、要素を追加したとき自動的に配列のサイズを変更してくれます。
これは「配列リスト」や「可変長配列」と呼ばれます。
配列リストの一般的な実装方法
配列リストは計算量 O(1) でのアクセスを備えており、
自身のサイズを必要に応じて変更できる配列です。
配列リストでは以下のことが行われています。
- 配列がいっぱいになったらサイズを 2 倍にする (最悪ケース)
- 挿入の実行時間: O(N)
- 配列がいっぱいになる状況は頻発しない
- 配列がいっぱいではないとき (最善ケース)
- 挿入の実行時間: O(1)
これは「償却計算量」の記事で詳しく説明しているので参考にしてみてください。
// 配列・リストを動的にサイズ変更する
ArrayList<String> merge(String[] words, String[] more) {
ArrayList<String> sentence = new ArrayList<String>();
for (String w : words) sentence.add(w);
for (String w : more) sentence.add(w);
return sentence;
}
面接試験ではこのような「配列リスト」のアルゴリズムを書けるようにしておいてください。
文字列連結の実行時間について

以下の文字列のリストを連結するコードの実行時間はどれくらいでしょうか。
String joinWords(String[] words) {
String sentence = ””;
for (String w : words) {
sentence = sentence + w;
}
return sentence;
}
連結のたびに新しい文字列 (オブジェクト) を生成しているため、
最初の 1 文字目から毎回コピーします。これはかなり非効率な処理といえます。
話を簡単にするために、文字列はすべて同じ長さ x であり 、文字列は n 個あるとしましょう。
- 最初の繰り返し処理
- x 文字分のコピーが要求される
- 2 回目の繰り返し処理
- 2x 文字分のコピーが要求される
- 3 回目の繰り返し処理
- 3x 文字分のコピーが要求される
- 最終的な計算量
- O(x + 2x + 3x + … + nx)
- = O(xn(n + 1) / 2)
- = O(xn^2)
- O(x + 2x + 3x + … + nx)
【Java】StringBuilder とは
Java では StringBuilder というクラスがあります。
このクラスの appned() を使うと、(裏側で) 連結後の文字列を配列で管理します。
配列が持っている前回の結果を使って次回の連結を行えるため、
毎回最初の文字からコピーする処理が不要になります。
String joinWords(String[] words) {
StringBuilder sentence = new StringBuilder();
for (String w : words) {
sentence.append(w);
}
return sentence.toStrng();
}
ハッシュテーブル や StringBuilder のようなクラスは個人で実装可能です。
文字列・配列を使いこなすいい練習になると思います。
文字列・配列の問題集

重複のない文字列
与えられた文字列の文字がすべてユニークである (重複する文字がない) ことを判定するアルゴリズムを実装してください。
答え
面談では、文字コードが ASCII か Unicode か確認しましょう。
今回は話を簡単にするため ASCII とします。
文字コードを仮定できない場合、記憶容量を大きく実装してください。
boolean 型の配列を作成する方法
※ 拡張 ASCII を使う場合、文字は 256 種類にしてください。
boolean isUniqueChars(String str) {
// 文字列の長さが文字の種類の個数を超えた場合 false
// ※ 128 文字の文字から 280 個のユニークな文字列を形成することはできない
if (str.length() > 128) return false;
boolean[] char_set = new boolean[128];
// ループ回数は文字数の 128 を超えることはない → 時間計算量は O(1) ともいえる
for (int i = 0; i < str.length(); i++) {
int val = str.charAt(i);
// この文字はすでに文字列の中で現れている
if (char_set[val]) {
return false;
}
char_set[val] = true;
}
return true;
}
文字列のサイズを n にする場合、コードの計算量は O(n) で、消費メモリは O(1) になります。
文字セットを仮定できない場合、
文字セットのサイズを c とすると空間計算量は O(c) となります。
時間計算量は O(min(c, n)) または O(c) になります。
ビットベクトルを用いる方法
アルファベット小文字だけ使用するならば 26 種類です。
その場合は 32 ビット整数を 1 つ使うだけで済みます。
※ 32 ビットのうち、最大でも 26 ビットしか使わない
ビットベクトルを使うと、消費メモリを 1/8 に抑えることができます。
※ 128 / 26 = 8
boolean isUniqueChars(String str) {
int checker = 0;
for (int i = 0; i < str.length(); i++) {
// アルファベット番号の取得
int val = str.charAt(i) - 'a';
/*
* checker & (1 << val) の条件でビットを立てる
* ※ (1 << val) は二進数 1 を val だけ左にシフトして、右端を 0 埋めしている
* ※ & 条件は重複部分のビットを返却する
* → アルファベット番号桁の重複がなければ 0 が返却される
* → アルファベット番号桁の重複があれば 0 以外が返却される
*/
if ((checker & (1 << val)) > 0) {
return false;
}
/*
* (1 << val) | checker の条件でビットを立てて checker を上書きする
* → アルファベット番号桁のビットを 1 にして checker 保存
*/
checker |= (1 << val);
}
return true;
}
実装するために新たなデータ構造が使えない場合
- すべての文字について、他の文字と順番に比較する
- 計算時間は O(n^2)
- メモリ消費は O(1)
- 文字列の操作が許される場合
- 文字列をソートする: O(n log(n))
- 文字列の先頭から隣り合う 2 文字を比較していく
順列チェック
2 つの文字列が与えられたとき、
片方がもう片方の並び替えになっているかどうか判定するメソッドを実装してください。
答え
面談では「順列の比較で大文字・小文字の区別が必要か」聞いておきましょう。
※ たとえば「God」は「dog」の順列といえるのか?
空白文字が意味を持つかどうか、も考える必要があります。
※ 今回は「god 」と「dog」の順列は別物とします
また、異なる長さの文字列の場合、互いの順列になることはありません。
文字列をソートする
2 つの文字列が順列であれば、まったく同じ文字が使われています。
なのでソートして文字列比較をすればよいことになります。
String sort(String s) {
char[] content = s.toCharArray();
java.util.Arrays.sort(content);
return new String(content);
}
boolean permutation(String s, String t) {
// 順列は同じ長さでなければならない
if (s.length() != t.length()) {
return false;
}
// ソートして文字列比較
return sort(s).equlas(sort(t));
}
同じ文字の数を数える
2 つの文字列が順列であれば、登場する文字の頻度も一致します。
ハッシュテーブルのように動作する配列を作成し、各文字の頻度をマッピングします。
1 つ目の文字列の文字の頻度はインクリメントして、
2 つめの文字列の文字の頻度はデクリメントします。
順列の場合、インクリメント・デクリメントの回数が一致するはずです。
boolean permutation(String s, String t) {
// 順列は同じ長さでなければならない
if (s.length() != t.length()) {
return false;
}
// ASCII と仮定
int[] letters = new int[128];
for (int i = 0; i < s.length(); i++) {
letters[s.charAt(i)]++; // インクリメント
}
for (int i = 0; i < t.length(); i++) {
letters[t.charAt(i)]--; // デクリメント
// 負の値になったら即終了する
if (letters[t.charAt(i)] < 0) {
return false;
}
}
return true;
}
URLify
文字列内に出現するすべての空白文字を %20 に置換するメソッドを実装してください。
- ただし、文字列の後ろには、新たに文字を追加するためのスペースが十分にあること。
- ※ バッファサイズは気にしなくてもよい
- 追加したスペースを除く文字列には真の長さが与えられること
- 例
- 入力: “Mr John Smith “, 13
- 出力: “Mr%20John%20Smith”
答え
文字列の最後尾から先頭に向かって編集する方法があります。
こうするとバッファの後ろに追加のバッファを加えることができますし、
編集時に文字列を上書きする心配もありません。
これは文字列操作でよくあるアプローチです。
void replaceSpaces(char[] str, int trueLength) {
int spaceCount = 0;
int index = 0;
int i = 0;
// 空白文字の数を数える
for (i = 0; i < trueLength; i++) {
if (str[i] == ' ') {
spaceCount++;
}
}
// return する配列の index 設定
// 空白文字を 3 倍にする: 「 」を「%20」 にするため
index = trueLength + spaceCount * 2;
if (trueLength < str.length) {
// 文字列終端の空白を置換
str[trueLength] = '\0';
}
// 文字列の最後尾からループ処理
for (i = trueLength - 1; i >= 0; i--) {
if (str[i] == ' ') {
// 文字列を書き換える
str[index - 1] = '0';
str[index - 2] = '2';
str[index - 3] = '%';
index = index - 3;
} else {
// 空白文字がない場合、元の文字をコピーする
str[index - 1] = str[i];
index--;
}
}
}
回文の順列
与えられた文字列が「回文の順列になれるかどうか」判定するメソッドを実装してください。
回文とは、前から読んでも後ろから読んでも同じになる単語・フレーズのことです。
※ 辞書にない単語も OK
- 例
- 入力: “Tact Coa”
- 出力: True (順列: “taco cat”, “atco cta”, など)
答え
回文は「前方と後方で同じ文字列」になります。
文字列を前半部分の単語、後半部分の単語…と分けるためには、
含まれる文字の頻度は偶数になっている必要があります。
ただし中央文字の 1 文字のみ奇数になることが許容されます。
- 例えば “tactcoapapa” は…
- T が 2 個
- A が 4 個
- C が 2 個
- P が 2 個
- O が 1 個
- 回文の中央文字なので奇数 OK
- なので、回文の順列である
このように与えられる文字列の「定義の特徴」を検討することは重要です。
解法1
ハッシュテーブルを使用して、各文字が何回出現して数えます。
ハッシュテーブルを走査し、奇数の文字数が複数存在しないことを確認します。
文字列の長さを N とすると、時間計算量 O(N) になります。
boolean isPermutationOfPalindrome(String phrase) {
int[] table = buildCharFrequencyTable(phrase);
return checkMaxOneOdd(table);
}
/*
* 文字数が奇数の文字が複数存在しないことを確認
*/
boolean checkMaxOneOdd(int[] table) {
boolean foundOdd = false;
for (int count : table) {
if (count % 2 == 1) {
if (foundOdd) {
return false;
}
foundOdd = true
}
}
return true;
}
/*
* 文字を数字に割り当てる
* ex) a -> 0, b -> 1, c -> 2
* 大文字小文字の区別は行わず、文字以外は -1 とする
*/
int getCharNumber(Character c) {
int a = Character.getNumericValue('a');
int z = Character.getNumericValue('z');
int val = Character.getNumericValue(c);
if (a <= val && val <= z) {
return val - a;
}
return -1;
}
/*
* 各文字が何回現れるかを数える
*/
int[] buildCharFrequency(String phrase) {
int[] table = new int[
Character.getNumericValue('z') -
Character.getNumericValue('a') + 1
];
for (char c : phrase.toCharArray()) {
int x = getCharNumber(c);
if (x != -1) {
table[x]++;
}
}
return table;
}
解法2
アルゴリズムは常に文字列全体を調べる必要があります。
なので Big O の計算量はこれ以上良くすることができません。
ですが「奇数チェックは最後じゃなくて途中にはさむ」とか、
「終わりに達するときには答えがわかっているようにする」といった改良・工夫は可能です。
Big O の表記上は同じでも、アルゴリズムによってわずかに早い・遅いがあるということです。
面談では「これが最適解」など断言しない方がいいと思われます。
boolean isPermutationOfPalindrome(String phrase) {
int countOdd = 0;
int[] table = new int[
Character.getNumericValue('z') -
Character.getNumericValue('a') + 1
];
for (char c : phrase.toCharArray()) {
int x = getCharNumber(c);
if (x != -1) {
table[x]++;
// 奇数
if (table[x] % 2 == 1) {
countOdd++;
// 偶数
} else {
countOdd--;
}
}
}
// 奇数の回数が 1 以下だったら true
return coundOdd <= 1;
}
解法3
実は文字数は重要じゃなくて「各文字の登場頻度が偶数・奇数か」だけ分かっていれば大丈夫です。
なのでそれだけを管理するビットベクトル整数が 1 つあればよいことになります。
26 種類あるアルファベットを前提とした場合、
0 から 26 までの整数でマップされたビットをつくります。
文字が登場するごとに、その文字に対応するビットを 0 → 1 したり 1 → 0 して切り替えます。
- ビットが全部 0 の場合
- 全ての文字の登場頻度が偶数なので回文である
- ビットが 1 箇所だけ 1 の場合
- 奇数は 1 箇所だけなので回文である
- ビットが 2 箇所以上 1 をもつ場合
- 奇数が複数あるので回文ではない
こういう風にビットを切り替えておけば、回文判定が可能になります。
ビットが 1 箇所だけ 1 が設定されていることを判定する方法
ここで、ビットがちょうど 1 箇所だけ 1 が設定されていることを判定する方法を紹介します。
ある数のビットベクトルと、ある数から 1 減算したビックベクトルの AND 条件をとることです。
※ ビット演算 AND (&) は左辺・右辺で共通の 1 があるビット箇所だけ 1 を返却します
- たとえば
00010000のような二進数があるとします。 - ここから 1 を減算すると
00001111が得られます。- 00010000
- 一箇所だけ 1 が設定されたパターン
- 00001111
- ビット演算
00010000 & 00001111の結果は00000000(二進数で 0)000100000 & 00001111 == 0は true になる- 1 箇所だけ 1 が設定されている: つまり回文
- 00010000
- 逆に、二進数
00101000から 1 を減算すると00100111が得られます。- 00101000
- 二箇所以上 1 が設定されたパターン
- 00100111
- ビット演算
00101000 & 00100111の結果は00100000(二進数で 32)00101000 & 00100111 == 0は false になる- 1 箇所だけ 1 が設定されていない: つまり回文ではない
- 00101000
boolean isPermutationOfPalindrome(String phrase) {
int bitVector = createBitVector(phrase);
// ビットが全部 0 だったら、全て偶数なので回文である
// ビットで 1 箇所だけ 1 だったら、奇数は 1 箇所なので回文である...を判定
return bitVector == 0 || checkExactlyOneBitSet(bitVector);
}
/*
* 文字列に対するビットベクトルを生成する
* 各文字の文字番号 i について i ビット目を切り替える
*/
int createBitVector(String phrase) {
int bitVector = 0;
for (char c : phrase.toCharArray()) {
int x = getCharNumber(c);
bitVector = toggle(bitVector, x);
}
return bitVector;
}
/*
* 整数の i ビット目を切り替える
*/
int toggle(int bitVector, int index) {
if (index < 0) return bitVector;
// 二進数 1 を index だけ左にシフトして、右端を 0 埋めする
int mask = 1 << index;
// その文字の登場頻度を管理するビットを見て、ビットを切り替える
if ((bitVector & mask) == 0) {
// mask | bitVector の条件でビットを立てて bitVector を上書きする
bitVector |= mask;
} else {
// -mask & bitVector の条件でビットを立てて bitVector を上書きする
bitVector &= -mask;
}
return bitVector;
}
/*
* 1 ビットだけが 1 になっているかどうかチェックする
*/
boolean checkExactlyOneBitSet(int bitVector) {
// 元の整数値と、元の整数値から 1 減算したもので AND 条件をとる
return (bitVector & (bitVector - 1)) == 0;
}
このアルゴリズムの実行時間は O(N) となります。
こういった解法を使えば「すべての可能な並べ替えを作成し、それらが回文かどうか確認」する。
…みたいなパワープレイを避けることができます。
そのようなアルゴリズムは O(N!) という最悪の実行時間になってしまい、
文字数が増えると実行そのものが (現実的に) 不可能になります。
回文かどうかを確認するために、すべての順列を生成する必要はありません。
一発変換
2 つの文字列を与えたとき、
一方の文字列に対して「文字の挿入、文字の削除、文字の置き換え」から 1 操作を行います。
そしてもう一方の文字列になれるかどうか判定するメソッドを実装してください。
- 例
- pale, ple
- true
- pales, pale
- true
- pale, bale
- true
- pale, bake
- false
- pale, ple
答え
一応、この問題は「ブルートフォース」なアルゴリズムで解くことができます。
各文字の挿入、各文字の削除、あらゆる文字の置き換えを行って、
考えるうる全ての文字列と比較することです。
しかしそれだと遅すぎるので注意してください。
- 置き換え
- pale と bale のような例です
- 文字数は一致します
- 異なる文字は 1 箇所だけ
- pale と bale のような例です
- 挿入
- aple と apple のような例です
- 文字列内でシフト場合を除いて、一致します
- 後者と比べて、前者の文字数は -1 になります
- aple と apple のような例です
- 削除
- aplle と aple のような例です
- 後者と比べて、前者の文字数は +1 になります
- これは「挿入」の逆なので、処理としてまとめることができます
- aplle と aple のような例です
文字列の長さに注目すれば、どの操作をするべきか絞ることができます。
文字列のチェックをする必要はありません。
boolean oneEditAway(String first, String second) {
// 置き換え
if (first.length() == second length) {
return oneEditReplace(first, second);
// 削除
} else if (first.length() + 1 == second length) {
return oneEditInsert(first, second);
// 挿入
} else if (first.length() - 1 == second length) {
return oneEditInsert(second, first);
}
// 与えられる 2 つ文字列の長さが違いすぎる場合、すぐに false を返すので O(1) になる
return false;
}
boolean oneEditReplace(String s1, String s2) {
boolean foundDifference = false;
for (int i = 0; i < s1.length(); i++) {
// 文字が一致しなかったら
if (s1.charAt(i) != s2.charAt(i)) {
// 2 ヶ所以上違ったら false を返却する
if (foundDifference) {
return false;
}
foundDifference = true;
}
}
return true;
}
/*
* s1 に 1 文字だけ挿入して s2 を作ることができるかどうか判定する
*/
boolean oneEditInsert(String s1, String s2) {
int index1 = 0;
int index2 = 0;
while (index2 < s2.length() && index1 < s1.length()) {
// 文字が一致しなかったら
if (s1.charAt(index1) != s2.charAt(index2)) {
if (index1 != index2) {
return false;
}
// s1 に 1 文字挿入したことにして index1++ はスキップする
index2++;
// 以後、index1 != index2 になる
} else {
index1++;
index2++;
}
}
return true;
}
短い方の文字列の長さを n とすると、このアルゴリズムの実行時間は O(n) になります。
文字列が同じ長さ、かつ長くなった分だけ実行時間が増加します。
メソッドをまとめる
oneEditReplace() と oneEditInsert() の処理は似ているので、まとめることもできます。
可読性は落ちるという指摘があるかもしれませんが、
こちらの方がコンパクトでコードの重複がないので優れたコードと主張する人もいるでしょう。
boolean oneEditAway(String first, String second) {
// 長さチェック
if (Math.abs(first.length() - second.length()) - 1) {
return false
}
// s1, s2 にどっちの文字列を入れるべきか判定する
String s1 = first.length() < second.length() ? first : second;
String s2 = first.length() < second.length() ? second : first;
int index1 = 0;
int index2 = 0;
boolean = foundDifference = false;
while (index2 < s2.length() && index1 < s1.length()) {
// 文字が一致しなかったら
if (s1.charAt(index1) != s2.charAt(index2)) {
if (foundDifference) return false;
foundDifference = true;
// 挿入時、文字列が短い方のポインタを動かす
if (s1.length() == s2.length()) {
index1++;
}
// 文字が一致したら、文字列が短い方のポインタを動かす
} else {
index1++;
}
// 文字列が長い方のポインタは常に動かす
index2++;
}
return true;
}
文字列圧縮
同じ文字が連続したら文字列圧縮を行うメソッドを実装してください。
たとえば aabcccccaaa はa2b1c5a3 になります。
もし圧縮した文字列が元の文字列より短くならなかった場合、元の文字列を返却してください。
与えられる文字列はアルファベットの大文字・小文字だけ想定してください。
答え
以下の処理を行えば OK です。
- 文字列を走査する
- 新しい文字列にコピーする
- 文字の繰り返しを数える
- 走査するごとに現在の文字と次の文字が同じかどうか確認する
- 違った場合は圧縮した結果を追加する
/*
* 良くない例
*/
String compressBad(String str) {
String compressedString = "";
int countConsecutive = 0;
// 最初に圧縮文字列を作成する
for (int i = 0; i < str.length(); i++) {
countConsecutive++;
// 次の文字が現在の文字と異なる場合
if (i + 1 >= str.length() ||
str.charAt(i) != str.charAt(i + 1)
) {
// 現在の文字を結果に追加する
compressedString += "" + str.charAt(i) + countConsecutive;
// 初期化
countConsecutive = 0;
}
}
// 入力文字列と圧縮文字列の短い方を返す
return compressedString.length() < str.length() ? compressedString : str;
}
元の文字列の長さが p で、連続する文字郡の数を k としましょう。
※ 例えば aabccdeeaa であれば、文字郡は abcdea なので k は 6 になります。
その場合、このコードの実行時間は O(p + k^2) になります。
StringBuilder を使わずに文字列の連結を行っているため O(n^2) もかかっているのです。
StringBuilder を使う例
String compress(String str) {
StringBuilder compressed = new StringBuilder();
int countConsecutive = 0;
// 最初に圧縮文字列を作成する
for (int i = 0; i < str.length(); i++) {
countConsecutive++;
// 次の文字が現在の文字と異なる場合
if (i + 1 >= str.length() ||
str.charAt(i) != str.charAt(i + 1)
) {
// 現在の文字を結果に追加する
compressed.apend(str.charAt(i));
compressed.apend(countConsecutive);
// 初期化
countConsecutive = 0;
}
}
// 入力文字列と圧縮文字列の短い方を返す
return compressed.length() < str.length() ? compressed : str;
}
先に最終的な長さをチェックする方法
最初に最終的な長さをチェックしておき、元の文字列より長ければ元の文字列を返すこともできます。
そうすることで、使用することない文字列をわざわざ作成する必要がなくなります。
また最初から StringBuilder で必要な容量を確保しておくことが可能になります。
StringBuilder は容量を超えると 2 倍の容量を確保する仕様なので、それを避けることができます。
ただし 2 回目のループが発生して、ほとんど同じコードが追加されてしまいます。
String compress(String str) {
// 最初に最終的な長さをチェックしておいて、元の文字列より長ければ元の文字列を返す
int finalLength = countCompression(str);
if (finalLength >= str.length()) return str;
// 初期の容量
StringBuilder compressed = new StringBuilder(finalLength);
int countConsecutive = 0;
for (int i = 0; i < str.length(); i++) {
countConsecutive++;
// 次の文字が現在の文字と異なる場合
if (i + 1 >= str.length() ||
str.charAt(i) != str.charAt(i + 1)
) {
// 現在の文字を結果に追加する
compressed.apend(str.charAt(i));
compressed.apend(countConsecutive);
// 初期化
countConsecutive = 0;
}
}
return compressed.toString();
}
int countCompression(String str) {
int compressedLength = 0;
int countConsecutive = 0;
for (int i = 0; i < str.length(); i++) {
int countConsecutive++;
// 次の文字が現在の文字と異なる場合
if (i + 1 >= str.length() ||
str.charAt(i) != str.charAt(i + 1)
) {
// 長さを増やす
compressedLength += 1 + String.valueOf(countConsecutive).length();
// 初期化
countConsecutive = 0;
}
}
return compressedLength;
}
行列の回転
N * N の行列に描かれた 1 つのピクセルが 4 バイト四方の画像があります。
追加の領域なしで、その画像を 90 度回転させるメソッドを実装してください。
答え
1 ピクセル 4 バイト四方とは 4 行 4 列の状態です。
この上下左右の幅のことをレイヤーと呼ぶとします。
行列を 90 度回転させるためには、レイヤーごとに移動させれば OK です。
// 行列の index ごとにレイヤーを入れ替える: O(N)
for i = 0 to n
temp = top[i];
top[i] = left[i];
left[i] = bottom[i];
bottom[i] = right[i];
right[i] = temp;
- レイヤーの回転
- 「上端」のレイヤーは「右端」のレイヤーとして移動させる
- 「右端」のレイヤーは「下端」のレイヤーとして移動させる
- 「下端」のレイヤーは「左端」のレイヤーとして移動させる
- 「左端」のレイヤーは「上端」のレイヤーとして移動させる
- 一番外側のレイヤーから内側のレイヤーに向かって、この入れ替え操作を行う
- ※ もしくは一番内側のレイヤーから外側のレイヤーに向かって、この入れ替え操作を行う
boolean rotate(int[][] matrix) {
if (matrix.length == 0 ||
matrix.length != matrix[0].length
) {
return false;
}
int n = matrix.length;
for (int layer = 0; layer < n / 2; layer++) {
int first = layer;
int last = n - 1 - layer;
for (int i = first; i < last; i++) {
int offset = i - first;
// 上端の値を保存
int top = matrix[first][i];
matrix[first][i] = matrix[last - offset][first]; // 左端 → 上端
matrix[last - offset][first] = matrix[last][last - offset]; // 下端 → 左端
matrix[last][last - offset] = matrix[i][last]; // 右端 → 下端
matrix[i][last] = top // 上端 → 右端 (保存された上端の値)
}
}
return true;
}
このアルゴリズムの計算量は O(N^2) です。
N^2 個の要素すべてに触る必要があるので、これ以上早くすることはできません。
ゼロの行列
M * N の行列について、要素が 0 であれば、
その行と列をすべて 0 にするようなアルゴリズムを書いてください。
答え
- 行列のすべての要素を順番に調べる
- 0 があれば、その行と列を 0 にしていくだけ
…ではありません。
もしその場で行と列を 0 で埋める処理をしてしまうと、
あっという間にすべての要素が 0 になってしまいます。
それを避けるために、もうひとつの行列を用意して 0 で埋める場所を記録することもできますが、
行列のすべての要素を 2 回走査する必要があるので O(MN) もメモリが必要になってしまいます。
実は「 2 行目 4 列目」のように、行と列どちらも分かっている必要はありません。
「 4 行目のどこかに 0 がある」
…のような情報さえあれば、その行列を 0 で埋めるだけになります。正確な 0 の位置は不要なのです。
void setZeros(int[][] matrix) {
// 0 が含まれるかどうか、位置を記録する
boolean[] row = new boolean[matrix.length];
boolean[] column = new boolean[matrix[0].length];
// 0 を含む行、および列のインデックスを保存
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (matrix[i][j] == 0) {
row[i] = true;
column[j] = true;
}
}
}
// 行を 0 で埋める
for (int i = 0; i < row.length; i++) {
if (row[i]) nullifyRow(matrix, i);
}
// 列を 0 で埋める
for (int j = 0; j < column.length; j++) {
if (column[j]) nullifyColumn(matrix, j);
}
}
void nullifyRow(int[][] matrix, int row) {
for (int j = 0; j < matrix[0].length; j++) {
matrix[row][j] = 0;
}
}
void nullifyColumn(int[][] matrix, int col) {
for (int i = 0; i < matrix.length; i++) {
matrix[i][col] = 0;
}
}
ビットベクトルを使う方法
boolean 配列の代わりにビットベクトルを使ったほうがメモリ効率がよくなります。
その場合の空間計算量は O(N) になります。
行配列の代わりに最初の行を使用して、
列配列の代わりに最初の列を使用することで、空間計算量をさらに O(1) に減らせます。
void setZeros(int[][] matrix) {
boolean rowHasZero = false;
boolean colHasZero = false;
/*
* matrix[i][j] に 0 があるとき
* 常に matrix[i][0] と matrix[0][j] を 0 に設定する
* そのあと matrix の残りを走査する
*/
// 最初の行に 0 があるかをチェック
for (int j = 0; j < matrix[0].length; j++) {
if (matrix[0][j] == 0) {
rowHasZero = true;
break;
}
}
// 最初の列に 0 があるかをチェック
for (int i = 0; i < matrix.length; i++) {
if (matrix[i][0] == 0) {
colHasZero = true;
break;
}
}
// 残りの行列に 0 があるかをチェック
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = 0;
matrix[0][j] = 0;
}
}
}
// 最初の列の値に基づいて、行を 0 で埋める
for (int i = 0; i < matrix.length; i++) {
if (matrix[i][0] == 0) {
nullifyRow(matrix, i);
}
}
// 最初の行の値に基づいて、列を 0 で埋める
for (int j = 0; j < matrix[0].length; j++) {
if (matrix[0][j] == 0) {
nullifyColumn(matrix, j);
}
}
// 最初の行を 0 で埋める
if (rowHasZero) {
nullifyRow(matrix, 0);
}
// 最初の列を 0 で埋める
if (colHasZero) {
nullifyColumn(matrix, 0);
}
}
void nullifyRow(int[][] matrix, int row) {
for (int j = 0; j < matrix[0].length; j++) {
matrix[row][j] = 0;
}
}
void nullifyColumn(int[][] matrix, int col) {
for (int i = 0; i < matrix.length; i++) {
matrix[i][col] = 0;
}
}
文字列の回転
isSubstring() は片方の文字列が、もう片方の文字列の一部分になっているかどうかを調べるメソッドです。
2 つの文字列 s1 と s2 が与えられたとき、isSubstring() を一度だけ使って s2 が s1 を回転させたものか判定するコードを書いて下さい。
※ たとえば waterbottle は erbottlewat を回転させています
答え
たとえば waterbottle を wat の後から回転させると、
erbottlewat という文字列が得られます。
- s1 = waterbottle
- s1 を x と y に切り分ける
- x = wat
- y = erbottle
- s1 = x + y
- s1 を x と y に切り分ける
- s2 = erbottlewat
- s2 = y + x
s1 を x と y に切り分ける方法があればよさそうです。
s1 を x と y に切り分ける際、どの場所で分けても y + x は x + y + x + y の部分文字列になります。
言い換えると s2 は s1 + s1 の部分文字列になります。
※ s1 + s1 = waterbottlewaterbottle
boolean isRotating(String s1, String s2) {
int len = s1.length();
/*
* s1 と s2 が同じ長さ
* かつ、空でないことをチェック
*/
if (len == s2.length() && len > 0) {
// s1 と s2 を連結
String s1s1 = s1 + s1;
return isSubstring(s1s1, s2);
}
return false;
}
isSubstring() の実行時間が O(A + B) と仮定すると、isRotation() の実行時間は O(N) になります。
CS シリーズ
次回
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント