
こんにちは。iQeda [@iQeeeda] です。
これからアルゴリズム性能を記述する Big O 記法について解説します。
Big O 記法を理解していなければアルゴリズム開発に苦労しますし、
ちゃんとしたテック企業のエンジニアは知ってて当然レベルの知識なので必ず押さえましょう。
Big O 記法の説明は長くなるので、今回は Big O 記法 の「概要」を説明します!
目次
ひらすら練習問題を解きたい人はこちらの記事。
計算量オーダーについて

時間計算量とは
時間計算量とは「物理的にかかる時間」を表します。
プログラムの実行時間・ファイルの転送時間という解釈で大丈夫です。
空間計算量とは
空間計算量とは「アルゴリズムを実行するのに必要なメモリ・スタック量」を表します。
Big O 記法とは [オーダー記法]
時間計算量でも、空間計算量でも、なにかしらのアルゴリズム性能を表すとき「Big O (ビッグ・オー) 記法」というもので「計算量の割合」を表現します。
ここでは「時間計算量」における Big O 記法の説明をします。
- Big O 記法は計算時間の上限を表す
- O の部分には「なにかしらの係数」が省略されているという意味がある (らしい)
- O(上限時間) で表現する
後述しますが Big θ (ビッグ・シータ) 記法というものもあって、
IT 業界では Big O 記法は「 Big θ 記法の意味で使われることが多い」点に気をつけて下さい。
上限以上の値を設定しても構わない
A さんの年齢は x 才で、130 才以上生きる人間は存在しない

計算量の話ですが、人間の年齢にたとえて説明します。
命題「 A さんの年齢は x 歳で、130 歳以上生きる人間は存在しない」があるとします。
このとき A さんの年齢は x <= 130 になるので「O(130)」と上限値を設定します。
しかし Big O 記法では x <= 1000000 でも x <= 10000000000 でも構わないものとします。
※ なぜなら x が 130 才以下なのは確実だから
なので「O(1000000) 」も「O(10000000000) 」も認められます。
上限が 130 以上であれば、どんな数字を設定しても構わないということです。
つまり O(N) のとき、N より大きい O(N^3) など設定しても OK ということになります。
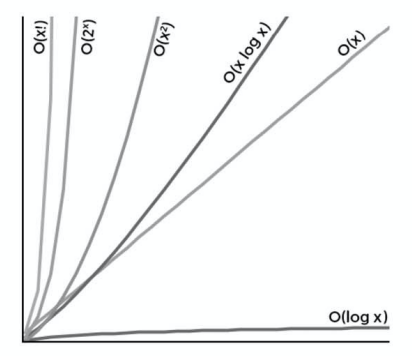
表現される性能 [オーダー] の種類
Big O で表現される計算量には様々な種類があり「オーダー」と呼びます。
そんなオーダーの一例を紹介します。
- O(1)
- データ量と関係なく、処理時間が一定のオーダー
- 決め打ちでデータ取得するのでもっとも早い
- いわゆる「定数時間」
- O(logN)
- 処理するたびにターゲットが絞られて早くなる魔法のようなオーダー
- O(N) に比べてかなり早い
- いわゆる「対数時間」
- O(N)
- データ量に応じて処理時間が比例するオーダー
- for 文で配列の中身を全部表示しようとするときがこれにあたる
- IT 業界ではこの処理速度が基準になる
- よってこれより処理が遅いときは何かマズいことが起きている
- いわゆる「線形時間」
- データ量に応じて処理時間が比例するオーダー
- O(NlogN)
- 学術的にはこちらが処理速度の基準とされているオーダー
- O(N) より少しだけ遅い
- いわゆる「準線形・線形対数時間」
- 学術的にはこちらが処理速度の基準とされているオーダー
- O(N^2)
- 二重ループ
- O(N) に比べてかなり遅い
- いわゆる「二乗時間」
- O(N^3)
- 三重ループ
- O(N) に比べてかなり遅い
- いわゆる「多項式時間」
- O(2^N)
- O(N) に比べてかなり遅い
- いわゆる「指数時間」
- O(N!)
- O(N) に比べてかなり遅い
- いわゆる「階乗時間」
- O(whp)
- width * height * person のような変数も使える、という例
最悪、時間計算量が O(N) を超えないアルゴリズムを書くようにしましょう。
O(1)
function log(arr) {
// 特定の要素にしかアクセスしない
console.log(array[0]);
console.log(array[1]);
}
log([1, 2, 3, 4]);
log([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]);
- O(1)
- 要素が多くなっても決まった処理しか行われない
- よって、処理時間は常に一定である
O(N)
function logAll(array) {
for (let i = 0; i < array.length; i++) {
// 全ての要素にアクセスする
console.log(array[i]);
}
}
logAll([1, 2, 3, 4, 5]);
logAll([1, 2, 3, 4, 5, 6]);
logAll([1, 2, 3, 4, 5, 6, 7]);
- O(N)
- データ量(N)に比例して計算量も増えていく
O(N^2)
function addAndLog(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
console.log(array[i] + array[j]);
}
}
}
// 9 パターンの組み合わせを表示: 3^2
addAndLog(["A", "B", "C"]);
// 16 パターンの組み合わせを表示: 4^2
addAndLog(["A", "B", "C", "D"]);
// 25 パターンの組み合わせを表示: 5^2
addAndLog(["A", "B", "C", "D", "E"]);
- O(N^2)
- 多重ループの構造だと「指数的爆発」が起きて非常に遅くなる
- データが多いとクラッシュする可能性もあるので注意
O(logN)
// 二分探索
function binarySearch(array, key) {
var low = 0;
var high = array.length - 1;
var mid;
var element;
while (low <= high) {
mid = Math.floor((low + high) / 2, 10);
element = array[mid];
if (element < key) {
low = mid + 1;
} else if (element > key) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}
// 第一引数の配列から、第二引数の値のインデックスを発見する
console.log(binarySearch([1, 2, 3, 4, 5, 6], 3));
- O(logN)
- データ量に対して、計算量を常に半分にしていくのですごく早い
- プログラムで書かれているのは「二分探索」というアルゴリズム
- データ量が 4000 あっても 12 回の処理で完了する
二分探索について
Big Ω 記法とは
「Big Ω (ビッグ・オメガ) 記法」というものもあります。
- Big Ω 記法では計算時間 [実行時間] の下限を表します
- Ω(下限時間) で表現する
下限以下の値を設定しても構わない
A さんの年齢は x 才で、0 才以下の人間は存在しない

また計算量の話ですが、人間の年齢にたとえて説明します。
命題「 A さんの年齢は x 歳で、0 歳以下の人間は存在しない」があるとします。
このとき A さんの年齢は 0 <= x になるので「Ω(0)」と下限値を設定します。
しかし Big Ω 記法では -1 <= x でも -1000000 <= x でも構わないものとします。
※ なぜなら x が 0 才以上なのは確実だから
なので「Ω(-1) 」も「Ω(-1000000) 」も認められます。
下限が 0 以下であれば、どんな数字を設定しても構わないということです。
つまり O(N) のとき、N より小さい O(log N) など設定しても OK ということになります。
Big θ 記法とは
最後に「Big θ (ビッグ・シータ) 記法」を紹介します。
Big O 記法はしばしば「Big θ 記法の意味で使われる」ので注意してください。
- Big O と Big Ω を併用する
- 「O(x) かつ Ω(x)」 なら θ(x) といえる
下限と上限を厳密に定義するのですね。
アルゴリズム実行時間の表現

アルゴリズムの実行時間は以下 3 つのケースがあります。
- 最善ケース
- 最悪ケース
- 期待ケース
今回は「クイックソート」という順番を入れ替えるアルゴリズムを例に説明します。
クイックソートの説明は以下リンク先がわかりやすいので紹介しておきます。
ざっくりクイックソートの説明をしておきます。
- ランダムに配列要素 (ピボット) を選ぶ
- ピボットより値が大きいグループ・ピボットより値が小さいグループを作成する
- 作成されたグループ内でも 1. 2. の作業を繰り返し行う
- グループがもう作れないところまで 3. の作業を行うと昇順のソート結果が得られる
最善ケースとは
配列要素すべての値が等しい場合、クイックソートの走査は一回で済みます。
これを「最善ケース」とします。
- O(N) と表現できる
最善ケースを試したいだけなら O(1) のオーダーで十分なので、あまり議論されません。
最悪ケースとは
配列 0 番目の要素が必ずピボットとして選ばれる仕様、かつ、
配列要素の値がすべて降順になっていた場合を「最悪ケース」とします。
最も大きい値をピボットとして選び続けてしまうので、非効率なグループ作成ばかりしてしまいます。
- O(N^2) と表現できる
期待ケースとは
最善でも最悪でもない、よくあるパターンを「期待ケース」とします。
- O(NlogN) と表現できる
空間計算量における Big O 記法

Big O 記法で PC メモリ領域・スタック領域を表すとき、以下のルールに従います。
- サイズ
nの配列を作るには…- O(n) のメモリ領域が必要
- サイズ
n * nの二次元配列を作るには…- O(n^2) のメモリ領域が必要
再帰的な呼び出しを行うときの注意点
再帰的な呼び出しを行うとき、スタック領域に注意してください。
O(n) のメモリ領域が必要になる例
下記の例だと、メモリ領域が O(4) 以上じゃないと実行できません。
sum(10000) だとメモリ領域が O(10000) 以上必要です。注意しましょう。
/*
* O(n) の実行時間が必要
* O(n) のメモリ領域が必要
*/
int sum(int n) {
if (n <= 0) {
return 0;
}
// 再帰的に sum() を O(n) 回呼び出して return する
// O(n) の空間計算量になる
return n + sum(n - 1);
}
// 実行
sum(4);
/*
* sum(4) -> sum(3) -> sum(2) -> sum(1) -> sum(0)
* ...と、呼び出されるごとにコールスタックに積まれてメモリを消費する
*/
O(1) のメモリ領域で済む例
下記の例だと、メモリ領域が O(1) で実行できます。
実行時間が O(n) だからといって、メモリ領域も O(n) 必要になるとは限らないのです。
/*
* O(n) の実行時間が必要
* O(1) のメモリ領域だけでよい
*/
int pairSumSequence(int n) {
int sum = 0;
for (int i = 0; i < n; i++) {
// ループ処理で pairSum() を O(n) 回呼び出す
// しかしコールスタック上に同時に存在させていないので、空間計算量は都度 O(1) でよい
sum += pairSum(i, i + 1);
}
return sum;
}
int pairSum(int a, int b) {
return a + b;
}
// 実行
pairSumSequence(4);
CS シリーズ
次回
前回
参考
- 一週間で身につくアルゴリズムとデータ構造|応用編第1日目:アルゴリズムと計算量
- 時間計算量とは – IT用語辞典
- 空間計算量とは – IT用語辞典
- オーダー記法・その1:使用例からの導入 – あざらしとペンギンの問題
- 計算量を具体的に見てみる – きしだのはてな
- オーダー記法の定義と大雑把な意味 | 高校数学の美しい物語
- 時間計算量 – cppreference.com
- [初心者向け] プログラムの計算量を求める方法 – Qiita
- ランダウの記号 – Wikipedia
- 計算量オーダーについて
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント