Develop に関する記事一覧

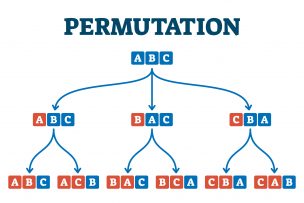
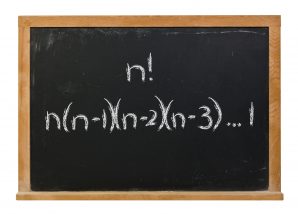階乗 0! が 1 になる理由説明は困難ですが、階乗を再帰的に定義するときに「 0! は 1 じゃないといけない」と直感的にわかります。今回は「階乗の再帰的定義」と「再帰と帰納の違い」について解説します。

プログラムでは「再帰処理」といって、同じ処理を何度も呼び出すことがあります。これは答えを導くために必要な「依存している値」も一緒に求める処理です。今回は「再帰」の基本的な考え方を「ハノイの塔」という問題で解説していきます。

前回、置換・順列を解説しました。こちらは「順序を考える」並べ方でした。この置換・順列は「並べ方はどうでもよくて、パターンだけ知りたいよ〜」…なときは使えません。今回は「順序を考えない」並べ方である「組み合わせ」について解説します！

物を並べるとき「何パターンの並べ方が考えられるか？」を検討するのは重要です。また、全部を並べるのか・一部だけ選んで並べるのか...で話は違います。今回はアルゴリズムで頻出する「順列」を解説します！

物を普通に数えると、人間はしばしば数え間違いを起こします。しかし、数えたい物の性質・構造を理解して「数えるルール」を作れば間違いを防げます。今回は「植木算」と「和の法則・積の法則」を学び、初歩的な「物の数え方」について学習しましょう。

ループ処理を作るとき、インクリメントされていく 0 以上の整数を使った処理が常に「真」になるか？それを数式で証明することはできますか？今回、0 以上のすべての整数についての主張を作ることができる証明方法「数学的帰納法」について解説します。

ケーニヒスベルグの橋という有名な一筆書きの問題があります。本当に一筆書きが可能か？「グラフ理論」というパリティのチェックで証明することが可能です。今回はそのグラフ理論について解説します。

余剰で偶数・奇数を求めることができますが、偶奇によってデータが壊れていないか？実行可能か？「目印」としてチェックすることができます。これをパリティといいます。今回は偶奇 (パリティ) の意味・その判定方法について解説します。

今回は剰余を使ったグループ分けについて解説します。なんらかの数字の法則性を発見できると、剰余でなんでもグループ分けが可能です！一度グループ分けが完了すると、複雑な数式でもパターンで答えが分かるようになります。