
こんにちは。iQeda [@iQeeeda] です。
前回、余剰について解説しました。
数字を 2 で割ったときの余剰が 0 か 1 かによって、
偶数・奇数の判定ができると書きましたが、「偶奇」にはどんなメリットがあるのでしょうか?
今回は偶奇 (パリティ) を使った判定方法について解説します。
【クイズ①】オセロで通信

手品師・弟子・客の 3 人がいます。
手品師は目隠しをしています。
テーブルに裏表ランダムのオセロが 7 個並んでいます。
手品師は色を見ることがきません。
例: ●○●○○●○
弟子はオセロを 1 つ追加します。
例: ●○●○○●○● (オセロを 1 つ追加)
客は 8 個のオセロを 1 つだけ裏返すか、何もしない行動をとることができます。
例: ●●●○○●○● (オセロを 1 つだけ裏返す)
例: ●○●○○●○● (何もしない)
手品師が 1 つだけ裏返したか、何もしなかったか、見破るにはどうしたらいいでしょうか?
答え
弟子はオセロが 7 個の時点で「黒」の数を数えます。
そして「黒」の偶奇によって、追加するオセロの色を決めます。
- もし黒が奇数だったら…
- 「黒」のオセロを追加する
- もし黒が偶数だったら…
- 「白」のオセロを追加する
このルールを適用すると、常に 8 個のオセロの「黒」の数は「偶数」で保たれます。
この先、客が取れる行動は以下 3 つです。
- 白を裏返す
- 黒が 1 つ増えて、黒が「奇数」になる
- 黒を裏返す
- 黒が 1 つ減って、黒が「奇数」になる
- 何もしない
- 何も変化しないので、黒は「偶数」のまま
手品師は、黒が「奇数」だったら「裏返した」と回答すればいいし、
黒が「偶数」だったら「何もしなかった」と回答すればよいことになります。
パリティとは (パリティのチェック)

このクイズはコンピュータ通信でいうところの「バリティ」で説明することができます。
パリティ (偶奇) とは、データが途中でおかしくなっていないかチェックする仕組みです。
二進法を使うと、オセロの白は「0」で、黒は「1」にあたります。
手品師は「受信者」で、弟子は「送信者」で、客は「通信を乱す雑音(ノイズ)」といえます。
※ 二進法については以下の記事で解説しています
バリティ・ビット
送信者が追加する 1 つのオセロは「パリティビット」と呼ばれます。
受信者はパリティを調べることで、ノイズで通信エラーが起きたか判定できます。
偶数だったらエラーはない、もしくは、奇数だったらエラーはない…
どちらのルールを適用するかは「送信者と受信者の間で決定」します。
バリティ・ビットで 2 つの集合に分割
7 個のオセロの並べ方は 2^7 で 128 パターンあります。
そのうち 64 パターンは黒が「偶数」、残りの 64 パターンは黒が「奇数」になります。
つまり 128 パターンを 2 つのグループに分けることができます。
弟子が追加するオセロは、どっちのグループに属しているかを表す「目印」ともいえます。
これはオセロが「黒か白か」 2 パターンの置き方しかないので 2 つのグループに大別できるのです。
【クイズ②】恋人探し

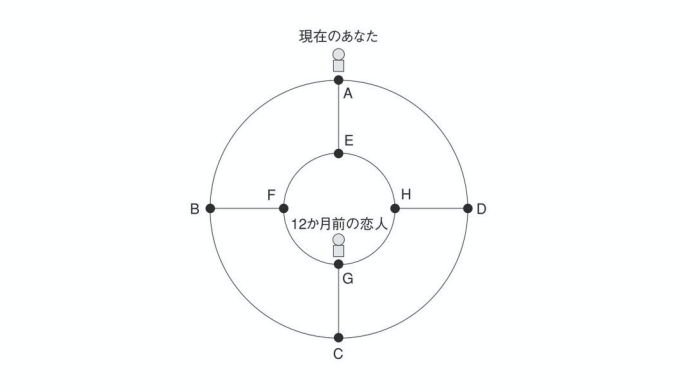
ある小さな国には A, B, C, D, E, F, G, H という 8 つの村があります。
村と村は次のように繋がっています。
あなたの恋人は 8 つの村のどこかにいますが 1 ヶ月ごとに隣の村に移動します。
(たとえば G の村にいるなら、来月は C, F, H いずれかの村に移動します)
恋人が 12 ヶ月前は G の村にいた…という情報だけ持っている場合、
今月、恋人が A の村にいる確率はいくつでしょう?
答え
表にすると答えはシンプルです。
| 移動回数 | 何ヶ月前 | 可能性がある村 |
|---|---|---|
| 0回目 | 12ヶ月前 | G |
| 1回目 (奇数回目) | 11ヶ月前 | C, F, H のどこか |
| 2回目 (偶数回目) | 10ヶ月前 | B, D, E, G のどこか |
| 3回目 (奇数回目) | 9ヶ月前 | A, C, F, H のどこか |
| 4回目 (偶数回目) | 8ヶ月前 | B, D, E, G のどこか |
| … | … | … |
恋人がどの村に向かうかはランダムなので、村の「道筋」をすべて検討するのは大変です。
なので、たどり着く可能性のある村だけを洗います。
奇数回目では A, C, F, H のいずれか (奇数村)、
偶数回目では B, D, E, G のいずれか (偶数村)、 にいることがわかります。
12 回目の移動は偶数回目なので A にいる可能性は 0 といえます。
奇数村・偶数村の 2 つのグループに分けられることに気づけるか?…がポイントです。
現在、どの村にいるかまでは分かりませんが、奇数村・偶数村どっちにいるかは判定できます。
常に「偶数村からの移動先は奇数村で、奇数村からの移動先は偶数村」になるので、
こうしたパリティ (偶奇) のチェックが適用できます。
【クイズ③】畳の敷き詰め

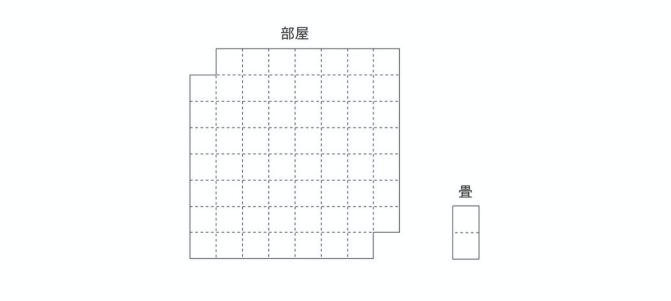
以下の部屋全体 (62半畳) に畳 (1畳) を敷き詰めることはできるでしょうか?
答え
1 畳は 2 半畳 で「偶数」です。また、部屋全体も 62 半畳の「偶数」です。
お互い偶数なので、敷き詰められる可能性はありそうです。
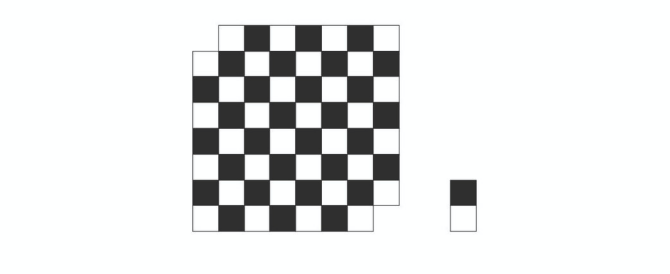
ここで部屋と畳を「白黒」の半畳で塗り分けてみましょう。
数えると、黒の半畳は 30 個・白の半畳は 32 個です。
1 畳は「黒の半畳」と「白の半畳」で構成されているため、
部屋の黒と白は同数じゃないと敷き詰めるとことはできません。
従って、部屋を畳で敷き詰めることは不可能です。
パリティを使って考える
計算する場合、黒の半畳に「+1」白の半畳に「-1」を割り当てます。
- 黒と白の合計値が 0 じゃない場合
- 敷き詰めることはできません
- 黒と白の合計値が 0 の場合
- 敷き詰められる可能性があります
可能性がある…という点に注意してください。
これは論理の「逆」なので、条件が入れ替わったからといって「真」になるとは限りません。
※ 論理については以下の記事で解説しています
今回の場合は 30 - 32 = 2 なので敷き詰めることはできない、と証明できます。
できないことを証明するのは簡単
パリティのチェックで NG がでると、「できない」ことの証明は簡単です。
試行錯誤して検証する必要がなくなります。
ただし、パリティのチェックが OK といって「常にできる」とは限らない点に注意です。
できることの証明の方が難しいのですね。
CS シリーズ
次回
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント