
こんにちは。iQeda [@iQeeeda] です。
プログラムでは「再帰処理」といって「関数の中でその関数をまた呼び出す」ことがあります。
これによって、欲しい答えを導くための「依存する値」を同時に求めることができます。
今回は「再帰」の基本的な考え方を「ハノイの塔」という問題で解説していきます。
ハノイの塔

3 本の細い柱 A, B, C が立っています。
柱 A には穴の開いた円盤が 6 枚積み重なっています。
円盤のサイズは全て異なり、
一番下の円盤が最も大きく、一番上の円盤が最も小さい円盤です。
その 6 枚の円盤を柱 B に移そうと思います。
ただし以下の条件を守ってください。
- 1 度に動かせる円盤は、柱の一番上に積まれた 1 枚だけ
- ある円盤の上に、それより大きい円盤を積んではいけない
1 枚の円盤をある柱からある柱へ動かすことを 1 手と考えると、
6 枚の円盤すべてを A から B に移すためには最低何手かかるでしょうか。
少ない円盤で考える
3 枚の円盤で考える
最初から 6 枚で考えるのは大変なので、まず 3 枚の場合で考えます。
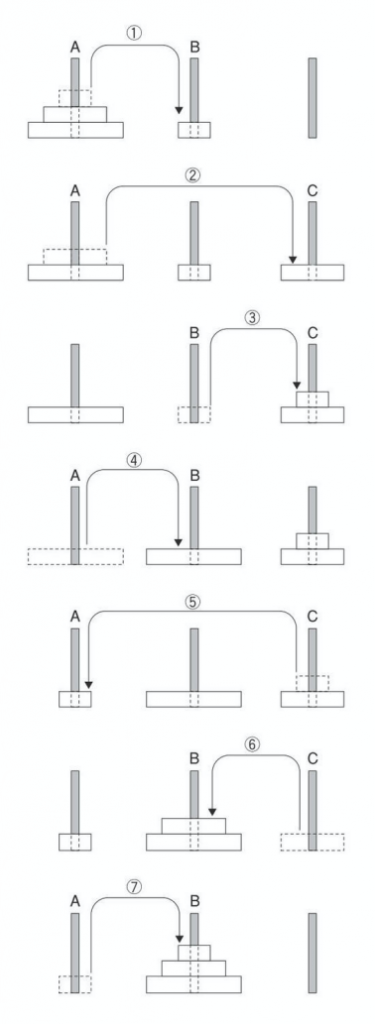
上記の画像を見てください。円盤を動かすフェーズは 3 つに別れています。
- ①, ②, ③
- 3 手かけて、柱 A の 2 枚の円盤を柱 C に移す
- ④
- 1 手かけて、柱 A の 1 枚の (最も大きい) 円盤を柱 B に移す
- ⑤, ⑥, ⑦
- 3 手かけて、柱 C の 2 枚の円盤を柱 B に移す
この「 2 枚の円盤を別の柱に移す」行為は 、2 枚の円盤で考えるときの条件と一緒です。
つまり「 3 枚の円盤」の問題は、「 2 枚の円盤」の問題の答えを使って解けることになります。
6 枚の円盤で考える
円盤が 6 枚の場合でも、先ほどと同じように考えることができます。
- ? 手かけて、柱 A の 5 枚の円盤を柱 C に移す
- 1 手かけて、柱 A の 1 枚の (最も大きい) 円盤を柱 B に移す
- ? 手かけて、柱 C の 5 枚の円盤を柱 B に移す
この「 5 枚の円盤を別の柱に移す」行為も 、5 枚の円盤で考えるときの条件と一緒です。
つまり「 6 枚の円盤」の問題は、「 5 枚の円盤」の問題が解けるなら解けることになります。
再帰的な構造
- 「 0 枚の円盤」の問題を解く
- 「 1 枚の円盤」の問題は、「 0 枚の円盤」の問題が解けるなら解ける
- 「 2 枚の円盤」の問題は、「 1 枚の円盤」の問題が解けるなら解ける
- 「 3 枚の円盤」の問題は、「 2 枚の円盤」の問題が解けるなら解ける
- 「 4 枚の円盤」の問題は、「 3 枚の円盤」の問題が解けるなら解ける
- 「 5 枚の円盤」の問題は、「 4 枚の円盤」の問題が解けるなら解ける
- 「 6 枚の円盤」の問題は、「 5 枚の円盤」の問題が解けるなら解ける
もし問題がこういった構造なのであれば、
0 枚の円盤の答えを使って 1 枚から 6 枚までの答えは「再帰的に」計算できそうです。
n 枚の円盤で考える

柱 A, B, C ではなく x, y, z という値で問題を捉えなおします。
- x
- 出発地の柱
- y
- 目的地の柱
- z
- 経由地点となる柱
円盤を動かすフェーズで「出発地」「目的地」「経由地点」の見方が変わるからです。
改めて「 n 枚の円盤を、柱 z を利用して柱 x から 柱 y へ移す」とはどういうことか整理します。
- n = 0 の場合
- 何もしなくてよい
- n > 0 の場合
n - 1枚の円盤を、柱 y を利用して柱 x から 柱 z へ移す- 1 枚の円盤を、柱 x から 柱 y へ移す
n - 1枚の円盤を、柱 x を利用して柱 z から 柱 y へ移す
n 枚の答えを導くには、やはり n - 1 枚の答えを再利用できそうです。
これを「再帰を使った表現」といいます。
漸化式とは
ここで、手数 H(n) という表現で式を立てることにします。
H(n)-
- (n = 0) の場合: 手数 0
- 0 枚の円盤を移す手数は 0
- (n > 0) の場合: 手数
H(n - 1) + 1 + H(n - 1)- これは「 n – 1 枚を解く手数 + 最大の円盤を動かず手数 + n – 1 枚を解く手数」のこと
- (n = 0) の場合: 手数 0
H(n) における H(n - 1) との関係式のことは「漸化式」といいます。
答え
H(0) の手数がわかり、 H(n - 1) から H(n) を作る方法がわかったので、
残る H(1) から H(6) まで順番に計算していけば 6 枚のときの手数がわかります。
| H(n) | 漸化式 | 意味 | 答え |
|---|---|---|---|
| H(0) | なし | 0 | 0 |
| H(1) | H(0) + 1 + H(0) | 0 + 1 + 0 | 1 |
| H(2) | H(1) + 1 + H(1) | 1 + 1 + 1 | 3 |
| H(3) | H(2) + 1 + H(2) | 3 + 1 + 3 | 7 |
| H(4) | H(3) + 1 + H(3) | 7 + 1 + 7 | 15 |
| H(5) | H(4) + 1 + H(4) | 15 + 1 + 15 | 31 |
| H(6) | H(5) + 1 + H(5) | 31 + 1 + 31 | 63 |
閉じた式とは
H(0) から H(6) の答えに規則性があれば、H(n) の答えも一般化できます。
| H(n) | 答え | 法則性 | つまり |
|---|---|---|---|
| H(0) | 0 | 1 – 1 | 2^0 – 1 |
| H(1) | 1 | 2 – 1 | 2^1 – 1 |
| H(2) | 3 | 4 – 1 | 2^2 – 1 |
| H(3) | 7 | 8 – 1 | 2^3 – 1 |
| H(4) | 15 | 16 – 1 | 2^4 – 1 |
| H(5) | 31 | 32 – 1 | 2^5 – 1 |
| H(6) | 63 | 64 – 1 | 2^6 – 1 |
H(n) は 2^n - 1 という式で表現できそうです。H(n) を n だけで表現する式のことは「 H(n) の閉じた式」といいます。
この閉じた式が正しいかどうかは「数学的帰納法」を使って証明できます。
数学的帰納法について
0 以上のすべての整数 n について証明することを「数学的帰納法」といいます。
数学的帰納法については以下の記事で詳しく解説しています。
ハノイの塔を解くプログラム

実際に動かした手数を表示する C 言語のプログラムは以下のとおりです。hanoi という関数の中で hanoi をまた呼び出すという「再帰処理」をしています。
# include <stdio.h>
# include <stdlib.h>
void hanoi (int n, char x, char y, char z);
void hanoi (int n, char x, char y, char z) {
if (n == 0) {
// 何もしない
} else {
// 再帰処理
hanoi(n - 1, x, z, y);
printf("%c->%c, ", x, y);
hanoi(n - 1, z, y, x);
}
}
int main (void) {
hanoi(6, 'A', 'B', 'C');
return EXIT_SUCCESS;
}
再帰的な構造を見つけだす

ハノイの塔のまとめになります。
- 円盤 3 枚という小さなスケールで検証した
- 「 n 枚」の問題は「 n – 1 枚」の答えを使って解けることを見つけた
- 再帰を使った表現
- 「 n 枚」の手数を「 n – 1 枚」の手数を使って表した
- 漸化式
大きい数字になると複雑化して問題が解けなくなってしまうことはよくありますが、
今回のように「大きい問題は、一回り小さい問題を使って表現できないか」考えてみてください。
これが「再帰」の基本的な考え方になります。
n 枚問題の手数が「 n – 1 枚を解く手数 + 最大の円盤を動かず手数 n – 1 枚を解く手数」であることを見つけられたのは「再帰的な構造を見つけ出した」といえます。
再帰的な構造さえ見つかれば「漸化式」にすれば OK です。
あわよくば、一発で答えを出せる「閉じた式」が得られると便利ですが、
漸化式だけでも地道に計算すれば具体的な答えが出せますし、問題の性質の把握に繋がります。
CS シリーズ
次回
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント