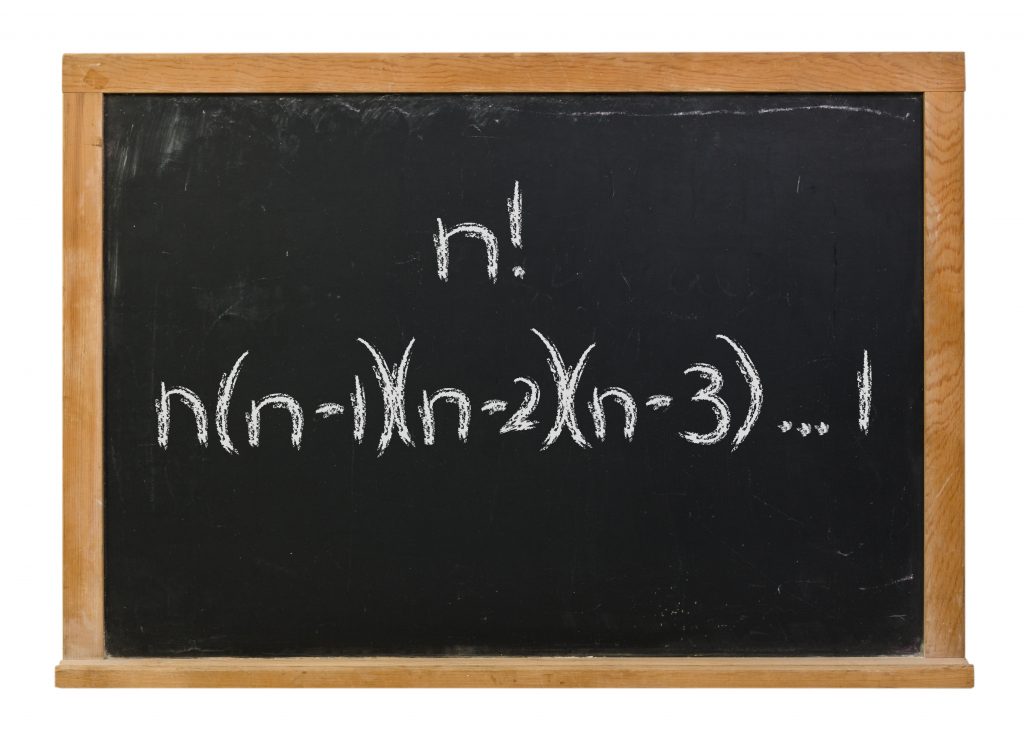
こんにちは。iQeda [@iQeeeda] です。
階乗 0! が 1 になる理由は「そういうルールだからあまり気にするな」と言ったことがあります。
実際、階乗を再帰的に定義しようと思ったとき、0! = 1 じゃないと矛盾が生じてしまうのです。
今回は「階乗の再帰的定義」と「再帰と帰納の違い」について解説します。
階乗の再帰的定義

まず「階乗」についての復習です。
階乗 n! は n * (n - 1) * (n - 2) * ... * 2 * 1 の意味でした。
そして階乗 0! は 1 を意味しました。
そして前回の復習ですが、
n を表現するために n – 1 という表現を使うことを「再帰」と言いました。
実は階乗も再帰的に定義することができます。
たとえば階乗 n! がある場合、以下のような再帰的な定義が可能です。
- n!
- (n = 0) の場合: 1
- (n > 0) の場合:
n * (n - 1)!- 再帰的な構造
具体的な階乗で考える
本当に再帰的な構造が存在するのか、具体的な階乗で検証してみましょう。
3!3 * 2!- つまり
3 * 2 * 1のこと
- つまり
2!の答えを再利用している
2!2 * 1!- つまり
2 * 1のこと
- つまり
1!の答えを再利用している
1!1 * 0!- つまり
1 * 1のこと
- つまり
0!の答えを再利用している
0!1
0! 以外は (n - 1) の答えを再利用していることがわかりますね。
また、再帰的な構造が成立させるには「 0! が 1 じゃないと辻褄が合わない」ことも分かります。
数学的帰納法との関連性

無数の証明ができる「数学的帰納法」では「基底」と「帰納」を行います。
基底は n = 0 の条件で P(n) を証明して、
帰納は k >= 0 の条件で P(k) が成り立つと仮定して P(k + 1) を証明します。
階乗の再帰的定義で最初に 0! が 1であることを定義するのは、
数学的帰納法の「基底」の考え方に近いものがありますね。
再帰と帰納の違い
再帰 (recursion) と帰納 (induction) の本質は同じです。
どちらも「大きな問題を、同じ形をした小さな問題に帰着させる」ことをしています。
両者の違いは「数の方向性」です。
再帰は「大きなものから、段々と小さいもの」に進んでいきますが、
帰納は「小さなものから、段々と大きいもの」に進んでいきます。
再帰的な数学的帰納法のプログラム
数学的帰納法の証明を C 言語でプログラムにすると以下のようになります。k = k + 1; していることから「小さなものから、段々と大きいもの」に進むことが分かります。
// p(0) から P(n) まで証明を行う
void prove(int n) {
int k;
k = 0;
printf("基底より、P(%d)が成り立ちます。\n", k);
while (k < n) {
printf("帰納より「P(%d)が成り立つならばP(%d)も成り立つ」といえます。\n", k, k + 1);
printf("したがって「P(%d)が成り立つ」といえます。\n", k + 1);
k = k + 1;
}
}
では、数学的帰納法の証明プログラムを再帰的に表現してみます。
void prove(int n) {
if (n == 0) {
printf("基底より、P(%d)が成り立ちます。\n", n);
} else {
// 再帰処理
prove(n - 1);
printf("帰納より「P(%d)が成り立つならばP(%d)も成り立つ」といえます。\n", n - 1, n);
printf("したがって「P(%d)が成り立つ」といえます。\n", n);
}
}
prove(n - 1); していることから「大きなものから、段々と小さいもの」に進むことが分かります。
「和の定義」を再帰的に定義する

n が 0 以上の整数であるとき、0 から n までの整数の和を再帰的に定義するとどうなるでしょうか。
0 から n までの整数の和を S(n) としましょう。S(n) を再帰的に定義すると以下のようになります。
S(n)- (n = 0) の場合: 0
- (n > 0) の場合:
n + S(n - 1)
S(n) の閉じた式
この問題に閉じた式も添えると S(n) = (n * (n + 1)) / 2 となります
これは以前「ガウス少年の主張」問題で解説しています。詳しくはそちらを参照してください。
CS シリーズ
次回
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント