こんにちは。iQeda [@iQeeeda] です。
物やデータを並べるとき「何パターンの並べ方が考えられるか?」を検討するのは重要です。
また、全部を並べるのか・一部だけ選んで並べるのか…で話は違います。
今回はアルゴリズムでも頻出する「順列」の基礎を解説します!
目次
置換とは

3 枚のカード A, B, C の順序を並べかえるとします。
※ 例えば、ABC, ACB, BCA … といったように
並べ方は全部で何通りあるでしょうか?
- ABC
- ACB
- BAC
- BCA
- CAB
- CBA
実際に並べてみると、答えは 6 通りです。
順序を考えて n 個のものを全て並べることを「置換」といいます。
置換の総数
では、計算結果をもとに置換の総数 (順序を考えて並べた総数) を求め方を説明します。
- 一枚目のカード
- 手持ちの 3 枚から 1 枚を選ぶので 3 通り
- 二枚目のカード
- 手持ちの 2 枚から 1 枚を選ぶので、一枚目の選び方に対して 2 通り
- 三枚目のカード
- 手持ちの 1 枚から 1 枚を選ぶので、一枚目・二枚目の選び方に対して 1 通り
「 1 枚目の選び方 * 2 枚目の選び方 * 3 枚目の選び方」で何通りあるか計算できます。
置換の総数は 3 * 2 * 1 で 6 通りと求めることができます。
階乗とは

次はカードを 5 枚に増やしてみましょう。
5 枚のカード A, B, C, D, E の置換の総数はいくつでしょう?
答えは 5 * 4 * 3 * 2 * 1 で 120 通りです。
この 5, 4, 3, 2, 1 と「 1 ずつ減っていく整数の掛け算」ですが、
簡単に 5! と表現できます。なので 5! = 5 * 4 * 3 * 2 * 1 です。
読み方は「5 の階乗」です。
階段のように下がっていく数を乗じている、と覚えましょう。
置換の総数の一般化
置換の総数を一般化してみましょう。 n 枚のカードの置換の総数はいくつになるでしょうか?
答えは n! です。
つまり n * (n - 1) * (n - 2) * ... * 3 * 2 * 1 のことです。
【問題】トランプの並べかた
ジョーカーを除くとトランプは 52 枚ありますが、一列に並べる方法は何通りでしょうか?
答え
答えは 52! で、計算すると 80658175170943878571660636856403766975289505440883277824000000000000 通りです。階乗は非常に数が大きくなるのが特徴です。
階乗の値
階乗の値について、いくつか例を示します。
| 階乗 | 意味 | 答え |
|---|---|---|
| 5! | 5 * 4 * 3 * 2 * 1 | 120 |
| 4! | 4 * 3 * 2 * 1 | 24 |
| 3! | 3 * 2 * 1 | 6 |
| 2! | 2 * 1 | 2 |
| 1! | 1 | 1 |
| 0! | 1 | 1 |
ゼロの階乗について
ゼロの階乗 0! の計算結果は 0 ではなく「 1 」になります。
これは深く考えるより「そういうルールだから」と思っておいてください。
そういうルールだからと言われても…
一応解説しました!
…が今はそんなに気にしなくていい、とだけ言っておきます。
順列とは

5 枚のカード A, B, C, D, E から 3 枚選び出し、
順序を考えて並べる場合の並べ方は何通りでしょうか?
- 一枚目のカード
- 手持ちの 5 枚から 1 枚を選ぶので 5 通り
- ※ 5 枚 – 1 枚目 + 1 で「 5 通り」を求めることができる
- 二枚目のカード
- 手持ちの 4 枚から 1 枚を選ぶので、一枚目の選び方に対して 4 通り
- ※ 5 枚 – 2 枚目 + 1 で「 4 通り」を求めることができる
- 三枚目のカード
- 手持ちの 3 枚から 1 枚を選ぶので、一枚目・二枚目の選び方に対して 3 通り
- ※ 5 枚 – 3 枚目 + 1 で「 3 通り」を求めることができる
「 1 枚目の選び方 * 2 枚目の選び方 * 3 枚目の選び方」で何通りあるか計算できるので、
並べ方は 5 * 4 * 3 で 60 通りとなります。
順列の総数
順序を考えて n 個のものを全て並べることを「置換」といいましたが、
順序を考えて n 個のものから k 枚 だけ選んで並べることを「順列」といいます。
順序を考える、ということ
置換・順序の「順序を考えて並べる」という考え方は大事なポイントです。
たとえば、並べ方「ABD」と「ADB」は同じカードを使っていますが、
置換・順序では「並べる順序が違うので、違う並べ方」としてカウントします。
これは順序を考えているからです。
順列の総数の一般化
n 枚のカードから k 枚のカードを選び出すとして、順列を一般化してみしょう。
- 一枚目のカード
- 手持ちの n 枚から 1 枚を選ぶので n 通り ( n – 0 通り)
- n 枚 – 1 枚目 + 1 で「 n – 0 通り」を求めることができる
- 二枚目のカード
- 手持ちの n – 1 枚から 1 枚を選ぶので、一枚目の選び方に対して n – 1 通り
- n 枚 – 2 枚目 + 1 で「 n – 1 通り」を求めることができる
- 三枚目のカード
- 手持ちの n – 2 枚から 1 枚を選ぶので、一枚目・二枚目の選び方に対して n – 2 通り
- n 枚 – 3 枚目 + 1 で「 n – 2 通り」を求めることができる
- k 枚目のカード
- n 枚 – k 枚目 + 1
順列の総数は (n - 0) * (n - 1) * (n - 2) * ... * (n - k + 1) 通りとなります。
n から引いている数は「 0 から k – 1 まで」変化していきます。
この「 0 から k – 1 まで」って一体何個あるんだ?…を考えるとき、
前回のブログ記事で紹介した「植木算」が使えます。
植木算は 0 番目の存在を忘れずちゃんと数えようという概念でしたが、
そこから「 0 から k – 1 まで」を数えると「 k 個」あることがわかります。
なので (n - 0) * (n - 1) * (n - 2) * ... * (n - k + 1) は k 個の項の掛け算です。
この n 個から k 個の項を選び出して順列の総数を求める行為は nPk と表記できます。
※ P は permutation の略です
まとめると、順列の総数を一般化すると nPk であり、
その意味は (n - 0) * (n - 1) * (n - 2) * ... * (n - k + 1) となります。
5 枚のカードから 3 枚選ぶ順列の総数
5 枚のカードから 3 枚選ぶ順列の総数は 5P3 と表記できます。5P3 は (5 - 0) * (5 - 1) * (5 - 2) なので、答えは 60 通りとなります。
置換の総数
置換の場合も P で表記できます。
置換は n と k の数が一致するので nPn になります。
順列の総数の値
順列の総数について、いくつか例を示します。
| 順列の総数 | 意味 | 答え |
|---|---|---|
| 5P5 | 5 * 4 * 3 * 2 * 1 | 120 |
| 5P4 | 5 * 4 * 3 * 2 | 120 |
| 5P3 | 5 * 4 * 3 | 60 |
| 5P2 | 5 * 4 | 20 |
| 5P1 | 5 | 5 |
| 5P0 | 1 | 1 |
項がゼロの順列の総数について
5P0 は 0 ではなく「1」 です。k が 0 のときは要注意です。
これもそういうルールだから仕方がないと思ってください。
階乗を使った順列の総数の表現
順列の総数は「階乗の表記方法」を使って nPk = n! / (n - k)! と表現することもできます。
たとえば 5P3 は 5! / (5 - 3)! になります。
これは要するに (5 * 4 * 3 * 2 * 1) / (2 * 1) のことで、
分母で分子を約分すると 5 * 4 * 3 になるので、5P3 の意味と一致することが分かります。
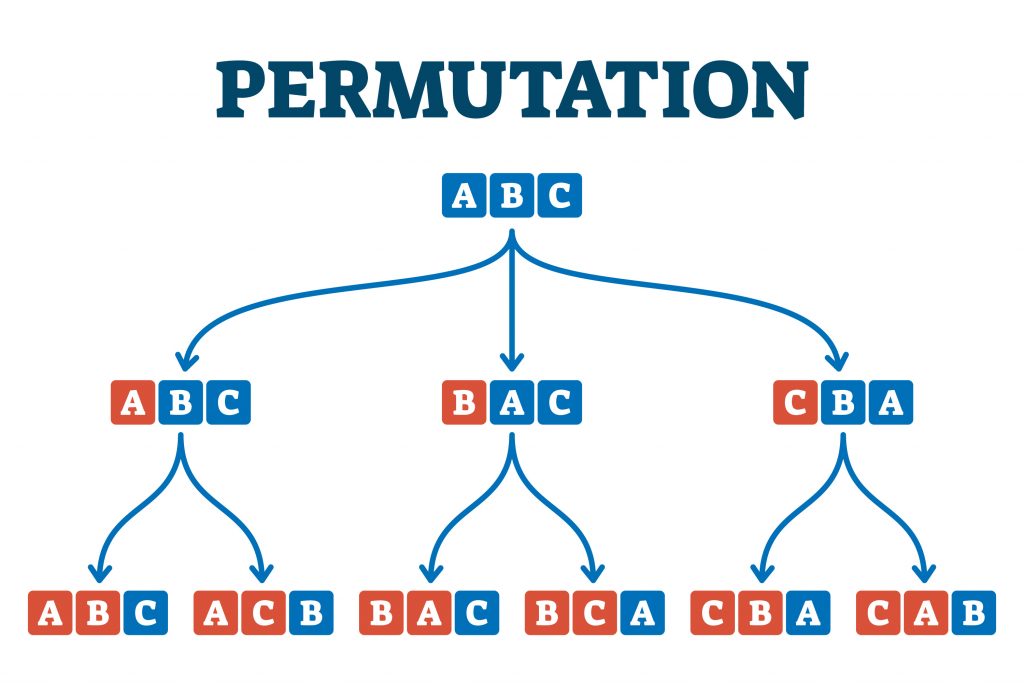
樹形図

重複なしの順列
A, B, C 3 枚のカードから 3 枚を選ぶ順列の場合、
同じカードを 2 回選ぶことはできません。
なので、2 枚目・ 3 枚目に選べる枚数は減っていきます。
これを「樹形図」というもので表現してみます。
root
├── A
│ ├── B
│ │ └── C
│ └── C
│ └── B
├── B
│ ├── A
│ │ └── C
│ └── C
│ └── A
└── C
├── A
│ └── B
└── B
└── A
根 (root) から 3 本の枝 (branch) が伸びていくように捉えてください。
それぞれの枝からは、枝が 2 本ずつ伸びています。
これは 2 枚目のカードの置き方が 2 通りあることを示しています。
最後の枝からは、枝が 1 本だけ伸びています。
この樹形図から、枝分かれの数は「3 → 2 → 1」と減っていくことが分かります。
重複ありで並べる場合
3 種類のカードから「重複を許して」3 枚並べる場合の樹形図はどうなるでしょうか?
あるカードを選んでも、そのカードは減らない場合のことです。
root
├── A
│ ├── A
│ │ ├── A
│ │ ├── B
│ │ └── C
│ ├── B
│ │ ├── A
│ │ ├── B
│ │ └── C
│ └── C
│ ├── A
│ ├── B
│ └── C
├── B
│ ├── A
│ │ ├── A
│ │ ├── B
│ │ └── C
│ ├── B
│ │ ├── A
│ │ ├── B
│ │ └── C
│ └── C
│ ├── A
│ ├── B
│ └── C
└── C
├── A
│ ├── A
│ ├── B
│ └── C
├── B
│ ├── A
│ ├── B
│ └── C
└── C
├── A
├── B
└── C
その場合の樹形図は根・すべての枝から 3 本の枝が伸びるようになります。
数える物の性質によってはこのように変化することを知っておきましょう。
CS シリーズ
次回
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント