
こんにちは。タクマ™ [@suwaru_blog] です。
前回、命題について解説しました。
今回は論理式という「命題の演算」で真偽の変化を見てみましょう。
そして真理値表というもので論理を解きほぐしていきます。
否定
ある命題に対して「…ではない」という命題をつくる演算のことを「否定(not)」と呼びます。
- 命題
- 乗車日は日曜日である
- 否定
- 乗車日は日曜日ではない
否定の論理式
論理演算子 (論理記号) は「ノット A」と呼びます。
- ¬A
否定の真理値表
演算子の定義・証明に使われる表のことを「心理値表」と言います。
| A | ¬A |
|---|---|
| true | false |
| false | true |
- 命題 A が true のとき
- 命題 ¬A は false である
- 命題 A が false のとき
- 命題 ¬A は true である
二重否定
否定を二回すると、元に戻ります。
- 命題
- 乗車日は日曜日である
- 二重否定
- 乗車日は日曜日ではない、ではない
- つまり「乗車日は日曜日である」と同じ
- 乗車日は日曜日ではない、ではない
二重否定の真理値表
| A | ¬A | ¬¬A |
|---|---|---|
| true | false | true |
| false | true | false |
- 命題 A が true のとき
- 命題 ¬A は false である
- 命題 ¬¬A は true である
- 命題 A が false のとき
- 命題 ¬A は true である
- 命題 ¬¬A は false である
論理積

ある命題 2 つを組み合わせて、
「A かつ B」という命題をつくる演算のことを「論理積(and)」と呼びます。
- 命題
- 年齢が 6 歳以上である
- 乗車日は日曜日である
- 論理積
- 年齢が 6 歳以上であり、かつ、乗車日は日曜日である
論理積の論理式
論理演算子 (論理記号) は「A アンド B」と呼びます。
A ∧ B- A と B の両方が true の場合だけ true となる命題
論理積の真理値表
命題が A と B の 2 つなので、組み合わせが 2^2 で 4 パターンあります。
| A | B | A ∧ B |
|---|---|---|
| true | true | true ∧ true → true |
| true | false | true ∧ false → false |
| false | true | false ∧ true → false |
| false | false | false ∧ false → false |
¬(A ∧ B)
「A かつ B ではない」
| A | B | ¬(A ∧ B) |
|---|---|---|
| true | true | ¬(true ∧ true) → ¬( true) → false |
| true | false | ¬(true ∧ false) → ¬(false) true |
| false | true | ¬(false ∧ true) → ¬(false) → true |
| false | false | ¬(false ∧ false) → ¬(false) → true |
論理和
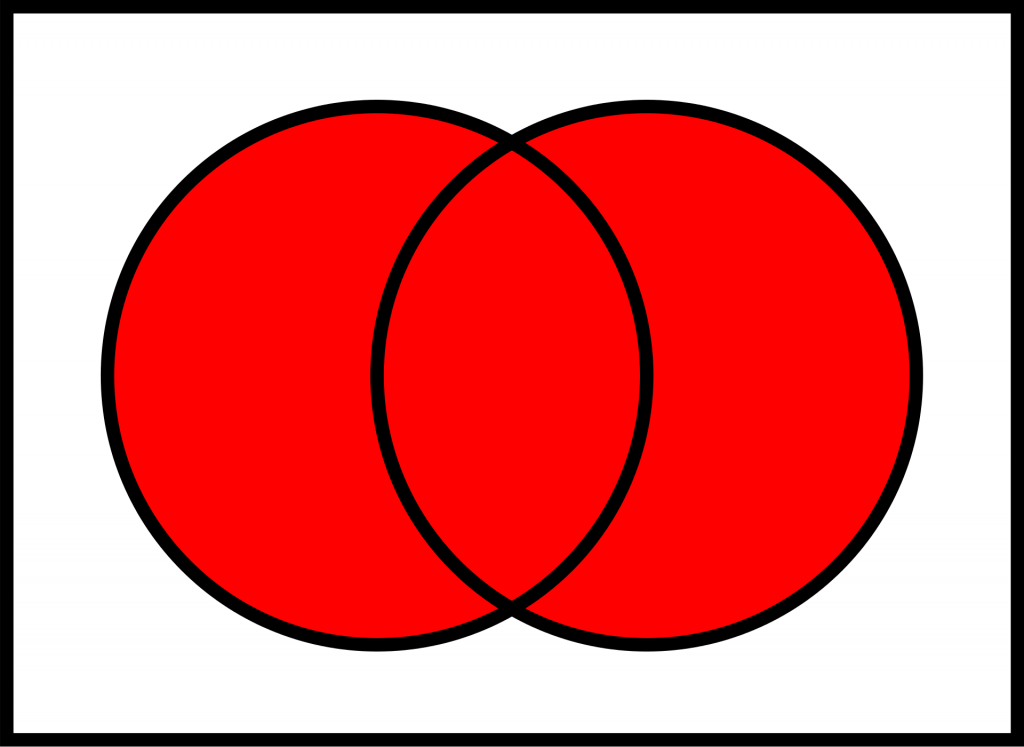
ある命題 2 つを組み合わせて、
「A または B」という命題をつくる演算のことを「論理和(or)」と呼びます。
- 命題
- クーポン券 A を持っていると割引が適用される
- クーポン券 B を持っていると割引が適用される
- 論理和
- クーポン券 A または B を持っていると割引が適用される
論理和の論理式
論理演算子 (論理記号) は「A オア B」と呼びます。
A ∨ B- A と B どちらか片方でも true のとき true となる命題
- A と B の両方が false ときだけ false となる命題、とも言える
論理和の真理値表
| A | B | A ∨ B |
|---|---|---|
| true | true | true ∨ true → true |
| true | false | true ∨ false → true |
| false | true | false ∨ true → true |
| false | false | false ∨ false → false |
(¬A) ∨ (¬B)
「A ではない、 または B ではない」
| A | B | (¬A) ∨ (¬B) |
|---|---|---|
| true | true | (¬true) ∨ (¬true) → false ∨ false → false |
| true | false | (¬true) ∨ (¬false) → false ∨ true → true |
| false | true | (¬false) ∨ (¬true) → true ∨ false → true |
| false | false | (¬false) ∨ (¬false) → true ∨ true → true |
ド・モルガンの法則
先程、紹介した以下の 2 つの命題は同じ真理値表になっています。
| A | B | ¬(A ∧ B) | (¬A) ∨ (¬B) |
|---|---|---|---|
| true | true | false | false |
| true | false | true | true |
| false | true | true | true |
| false | false | true | true |
また、以下 2 つの命題も同じ真理値表になっています。
- 「A または B ではない」
- 「A ではない、 かつ B ではない」
| A | B | ¬(A ∨ B) | (¬A) ∧ (¬B) |
|---|---|---|---|
| true | true | ¬(true ∨ true) → ¬(true) → false | (¬true) ∧ (¬true) → false ∧ false → false |
| true | false | ¬(true ∨ false) → ¬(true) → false | (¬true) ∧ (¬false) → false ∧ true → false |
| false | true | ¬(false ∨ true) → ¬(true) → false | (¬false) ∧ (¬true) → true ∧ false → false |
| false | false | ¬(false ∨ false) → ¬(false) → true | (¬false) ∧ (¬false) → true ∧ true → true |
この法則性は「双対性」という言葉で説明できます。
双対性
以下それぞれを交換することで、双対性のある論理式を作成できます。
- true と false
- A と ¬A
- ∧ と ∨
たとえば A ∧ B から、双対性を基にした (¬A) ∨ (¬B) を作成できます。
この (¬A) ∨ (¬B) は ¬(A ∧ B) と等しくなります。
※ ¬(A ∧ B) は元の論理式 A ∧ B の否定形
これが「ド・モルガンの法則」が言っている形になります。
双対性で「元の論理式全体を否定した論理式」と同じ真理値表をもつ論理式を導くことができます。
排他的論理和
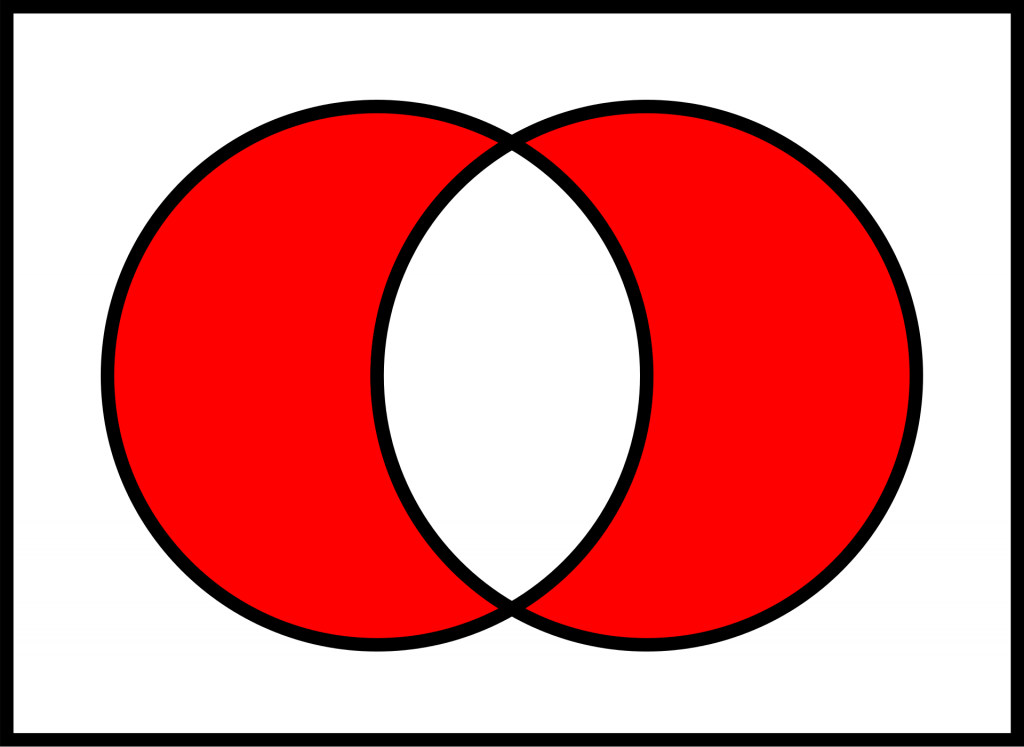
論理和の「または」とニュアンスが違って、
両方の条件を満たすことは想定しない「または」の使い方があります。
ある命題 2 つを組み合わせて、
「A または B (だが両方の条件は満たさない)」という命題をつくる演算のことを「論排他的理和(exclusive or)」と呼びます。
- 命題
- 彼は現在東京にいる
- 彼は現在大阪にいる
- 論理和
- 彼は現在東京にいる、または、彼は現在大阪にいる
- ※ 同じ人間が違う場所に同時に存在することはありえない
排他的論理和の論理式
論理演算子 (論理記号) は A ⊕ B と表現できます。
- A ⊕ B
- A と B が異なるときだけ true となる命題
- A と B の両方が true とき false となる命題、とも言える
排他的論理和の真理値表
| A | B | A ⊕ B |
|---|---|---|
| true | true | true ⊕ true → false |
| true | false | true ⊕ false → true |
| false | true | false ⊕ true → true |
| false | false | false ⊕ false → false |
¬(A ⊕ B)
「A または B ではない」
| A | B | ¬(A ⊕ B) |
|---|---|---|
| true | true | ¬(true ⊕ true) → ¬(false) → true |
| true | false | ¬(true ⊕ false) → ¬(true) → false |
| false | true | ¬(false ⊕ true) → ¬(true) → false |
| false | false | ¬(false ⊕ false) → ¬(false) → true |
等値
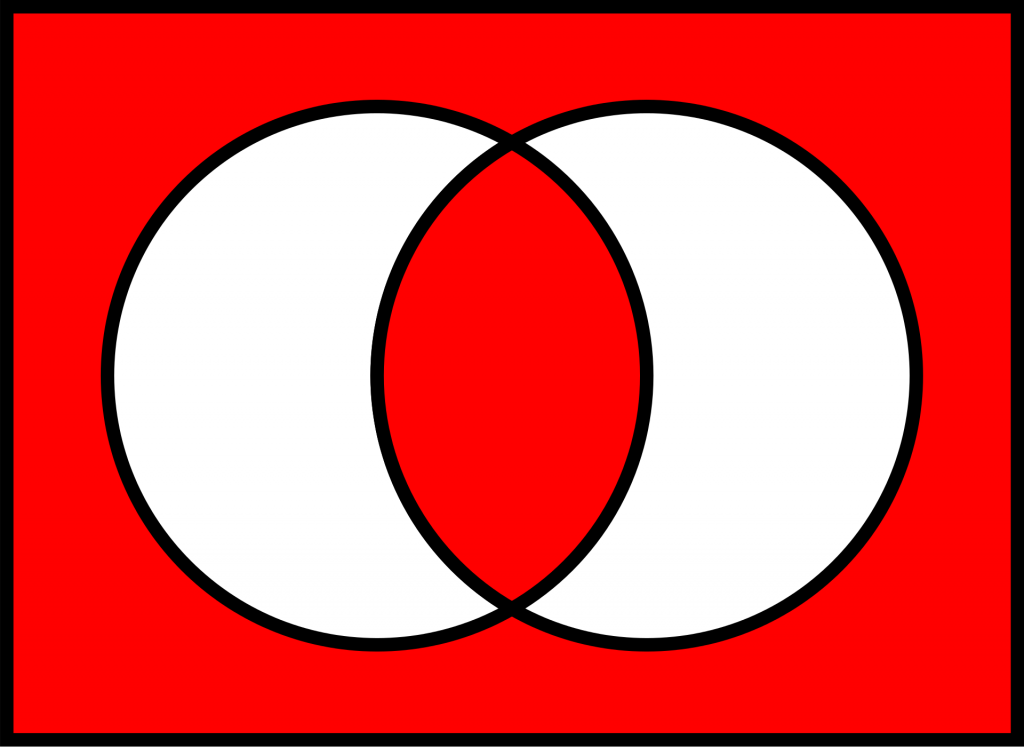
ある命題 A と B があるとき「A と B は等しい」という論理式は A = B と表現できます。
- 命題
- A と B は等しい
等値の真理値表
| A | B | A = B |
|---|---|---|
| true | true | true = true → true |
| true | false | true = false → false |
| false | true | false = true → false |
| false | false | false = false → true |
恒真命題
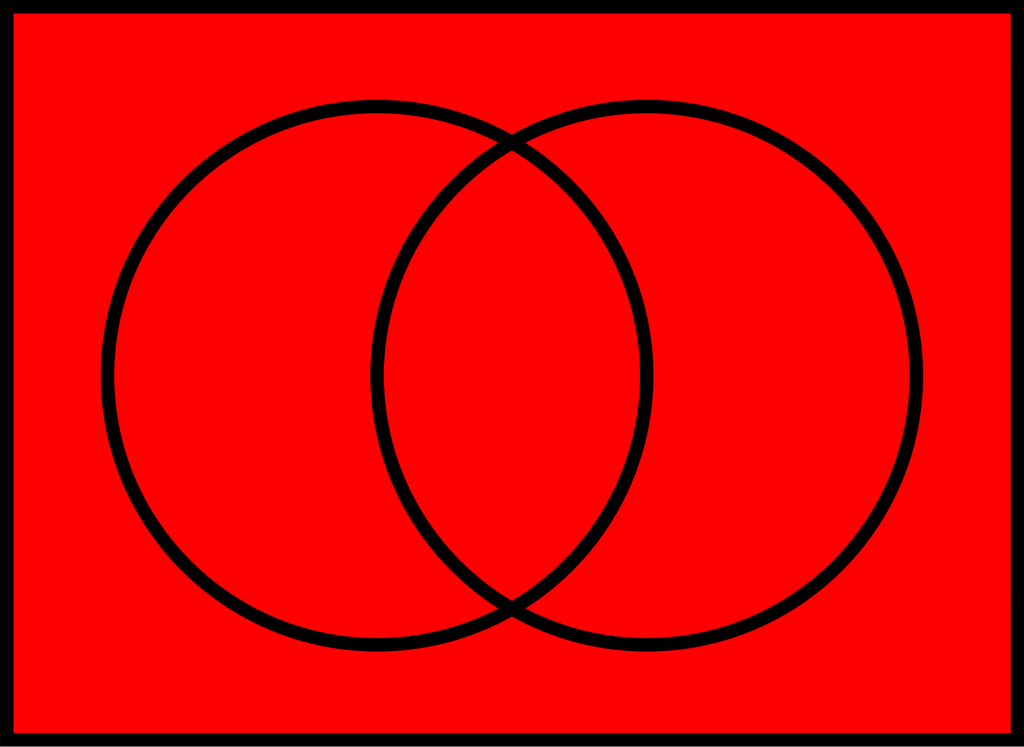
実は「A = B」と「¬(A ⊕ B)」の結果は同じになっています。
| A | B | ¬(A ⊕ B) | A = B |
|---|---|---|---|
| true | true | true | true |
| true | false | false | false |
| false | true | false | false |
| false | false | true | true |
この 2 つの命題を (¬(A ⊕ B)) = (A = B) という = で繋いだ命題をつくった場合、
A と B の真偽がなんであろうと、結果が true になってしまいます。
こういった常に true になってしまう命題のことを「恒真命題」といいます。
含意
ある命題 2 つを組み合わせて「A ならば B」という命題をつくる演算のことを「含意」と呼びます。
- 命題
- 乗客の年齢は 10 歳以上である
- 乗客の年齢は 6 歳以上である
- 論理和
- 乗客の年齢が 10 歳以上ならば、乗客の年齢は 6 歳以上である
含意の論理式
論理演算子 (論理記号) は A ⇒ B と表現できます。
- A ⇒ B
含意の真理値表
| A | B | A ⇒ B |
|---|---|---|
| true | true | true ⇒ true → true |
| true | false | true ⇒ false → false |
| false | true | false ⇒ true → true |
| false | false | false ⇒ false → true |
- A が true のとき
- B が false のとき
A ⇒ Bは false になる
- B が false のとき
- A が false のとき
A ⇒ Bは常に true になる- 前提条件 A が false なのに、 B の真偽がどちらであれ結果が true になるのは何故?
- 日本語の「ならば」には 2 種類の文脈があるので、混乱してしまう…
2 種類の「ならば」
A = B の等値でも「ならば」という言い回しを使うことができます。
A = Bが true になる条件- A が true 「ならば」 B も true である
- また、 A が false 「ならば」 B も false である
A ⇒ Bが true になる条件- A が true 「ならば」 B も true である
- しかし、 A が false 「ならば」 B は true/false どちらでもよい
(¬A) ∨ B
「A ではない、または B」
| A | B | (¬A) ∨ B | A ⇒ B |
|---|---|---|---|
| true | true | (¬true) ∨ true → false ∨ true → true | true |
| true | false | (¬true) ∨ false → false ∨ false → false | false |
| false | true | (¬false) ∨ true → true ∨ true → true | true |
| false | false | (¬false) ∨ false → true ∨ false → true | true |
「A が否定されている論理和」と「含意」の真理値表は一致します。
- A ではない、または B
- A ならば B
B ⇒ A
「B ならば A」
| A | B | B ⇒ A | A ⇒ B |
|---|---|---|---|
| true | true | true ⇒ true → true | true |
| true | false | false ⇒ true → true | false |
| false | true | true ⇒ false → false | true |
| false | false | false ⇒ false → true | true |
逆
A ⇒ B から B ⇒ A にしたものを「逆」といいます。
真理値表を見ればわかるとおり、必ずしも結果は一致しません。
つまり A ⇒ B が真になったからといって、B ⇒ A が真になるとは限りません。
(¬B) ⇒ (¬A)
先程「A ⇒ B と (¬A) ∨ B の真理値表は同じという話」をしましたが、
そのルールを当てはめると (¬B) ⇒ (¬A) と ¬(¬B) ∨ (¬A) の真理値表も同じなります。
そして ¬(¬B) ∨ (¬A) は A ⇒ B と真理値表が一致します。
| A | B | (¬B) ⇒ (¬A) | ¬(¬B) ∨ (¬A) | A ⇒ B | (¬A) ∨ B |
|---|---|---|---|---|---|
| true | true | (¬true) ⇒ (¬true) → false ⇒ false → true | ¬(¬true) ∨ (¬true) → true ∨ false → true | true | true |
| true | false | (¬false) ⇒ (¬true) → true ⇒ false → false | ¬(¬false) ∨ (¬true) → false ∨ false → false | false | false |
| false | true | (¬true) ⇒ (¬false) → false ⇒ true → true | ¬(¬true) ∨ (¬false) → true ∨ true → true | true | true |
| false | false | (¬false) ⇒ (¬false) → true ⇒ true → true | ¬(¬false) ∨ (¬false) → false ∨ true → true | true | true |
対偶
さらに (¬B) ⇒ (¬A) は A ⇒ B の「対偶」といいます。
含意関係にある A と B を入れ替えて、ABそれぞれに否定を付けると同じ意味になるのです。
説明すべてを理解する、じゃなく公式や法則を理解する
ぶっちゃけ日本語ですべて理解するのは大変です…
真理値表をざっと見ておいて、公式や法則が理解できれば OK です。
Wikipedia の「論理演算」にたくさん図が載っていて、解説が豊富です。
見ておいて損はないと思います。
CS シリーズ
次回
前回
お仕事ください!
僕が代表を務める 株式会社 EeeeG では Web 制作・システム開発・マーケティング相談を行っています。 なにかお困りごとがあれば、Twitter DM や Web サイトからお気軽にご相談ください。
カテゴリ「CS」の最新記事


 【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス
【ロードマップ】文系の元ラーメン屋が学んだコンピュータサイエンス  【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説
【データ構造】「木とグラフ・探索アルゴリズム」をわかりやすく解説  【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】
【データ構造】キューとスタックの使い方を解説!【実用例たっぷり】  【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】
【データ構造】連結リスト・ランナーテクニックを解説!【頻出問題】  【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】
【データ構造】面談対策!文字列・配列の問題解説【ハッシュテーブル】  TerraformによるLinodeインスタンス新規作成サンプル
TerraformによるLinodeインスタンス新規作成サンプル  【Fingerprint】CircleCIがSSHできない問題解決
【Fingerprint】CircleCIがSSHできない問題解決  【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正
【Laravel】セッションタイムアウト後のログイン処理で前回URLに遷移するバグ修正  M1 Mac(2021)でanyenv/phpenvの初期設定!
M1 Mac(2021)でanyenv/phpenvの初期設定! 










コメント